About Circles 11/22

(Last Edit: 11/24/2025)


Confused about the meaning of a matrix basis. Can an \(nxn\) matrix be a basis vector? What even is a basis vector? We're back to the origin again.

If \(A = V D V^{-1}\) then setting \(M = V^{-T}\) allows us to write \(A\) as \[ A = \lambda_1 v_1 m_1^T + \lambda_2 v_2 m_2^T + \cdots + \lambda_n v_n m_n^T \] In fact this is an \(n\) dimensional basis that spans all posible matrices with the same eigenvectors. We can show this by observing that \([m_1, \cdots, m_n]^T [v_1, \cdots, v_n] = I \).

Copilot has reminded me to say that suppose \(v_1 m_1^T\) could be rewritten as the linear combination of \(c_2 v_2 m_2^T + \cdots + c_n v_n m_n^T\), then we could say \(-v_1 m_1^T + c_2 v_2 m_2^T + \cdots + c_n v_n m_n^T = 0\), and \(c_1 = -1\), so there is at least one non-trivial \(c_k\). If only the 0 solutions exist, we could not write one matrix as the linear combination of the other matrices. \[ c_1 v_1 m_1^T + \cdots + c_n v_n m_n^T = 0 \] We can show that for all \(k\) \[ \begin{align} c_1 v_1 (m_1^T v_k) + \cdots + c_n v_n (m_n^T v_k) &= 0 v_k\\ c_k v_k &= 0 v_k\\ c_k &= 0 \end{align} \] Therefore only the trivial solution exists, and we have a linearly independent basis.

We can construct a new matrix \(B\) by zeroing out the first coordinate, which we can do since we know the first eigenvectors of \(A\) and \(A^T\). Power Iterations on B would now collapse any vector along the \(v_1\) component, and we have chosen by construction to not touch any of the other eigenvalues. So the dominant scaling direction is now along \(v_2\).

The only other thing is that in the case where \(\lambda_1 = \lambda_2\) any eigenvector within the span of \(v_1\) and \(v_2\) would also have the same eigenvalue. So power iterations can not converge on the same eigenvector as we constructed it, but we will still have identified the same subspace associated with that eigenvalue. \[ \begin{align} B &= 0 v_1 m_1^T + \lambda_2 v_2 m_2^T + \cdots + \lambda_n v_n m_n^T\\ B &= A - \lambda_1 v_1 m_1^T \end{align} \] Our algorithm is now:

import phoebus_V9 as ph

A = ph.array([[1,2,3],
              [3,2,1],
              [3,2,2]])

def eig(A):
    b = ph.array([1,0,0]).T
    for i in range(0,100):
        b = A*b
        b = b/b.norm
    return(b)

v1 = eig(A)
m1 = eig(A.T)
s1 = v1.T*A*v1 #the first eigenvalue

A2 = A-s1*v1*m1.T
v2 = eig(A2)
s2 = v2.T*A*v2 #the second eigenvalue

The next task is to show that the second column of the QR iterations is effectively Power Iterations on the deflated transformation which has collapsed along the dominant eigenvector.

Finding the Line 11/09

We have not constructed this basis, and the mechanism of generating new eigenvectors does not yet exist. (That which is has already been...) If we succeed, then the question of what happens to eigenvalues under a matrix transpose can be answered.

Now \(Ax=b\) becomes \(V^{-1} A V x_v = y_v\), in the new basis. But we can go one step further. Consider just this part \(AV\), and that the columns of \(V\) are eigenvectors so \(A v_1 = \lambda_1 v_1\). \[ \begin{align} AV &= [Av_1, Av_2, \cdots, Av_n]\\ AV &= [\lambda_1 v_1, \lambda_2 v_2, \cdots, \lambda_n v_n]\\ AV &= [v_1, v_2, \cdots, v_n]\begin{bmatrix} \lambda_1 & & &\\ &\lambda_2& &\\&&\ddots&\\ &&&\lambda_n \end{bmatrix}\\ AV &= VD \end{align} \] If every vector \(x\) maps to a unique coordinate \(b = Ax\), then every \(b\) maps back to a unique \(x = A^{-1}b\). Since \(A\) spans dimension \(n\), and \(A^{-1}\) reverses that mapping, its columns must span dimension \(n\) as well. So, \(A^{-1}\) is also of full rank.

Returning to the question of the matrix transpose, we know that \[ A = V D V^{-1} \] Taking the transpose of both sides gives \[ A^T = V^{-T} D V^T \]
Now consider the matrix \(V^{-T}\). We know that \(V^{-1} V = I\) so taking the transpose gives \(V^T V^{-T}=I\), which says that the inverse of \(V^{-T}\) is \(V^T\), so both are of full rank.

We have just discovered that the columns of \(V^{-T}\) form the eigenvectors of \(A^T\), and shown that they are linearly independent. Since \(D\) is the same we know that the eigenvalues are also sorted in decreasing order. Now conditions 1 and 2 are satisfied and we have a complete Eigen-Basis for \(A^T\). So the transpose has no effect on the eigenvalues. Using this hypothetical basis as a guide, we will proceeed to show how \(A\) may be modified to remove the first eigenvalue, this will allow our existing Power Iteration algorithm to find the second eigenvector.

A simple proof 11/05

Take any two eigenvalue/eigenvector pairs: \[ \begin{align} Ax_1 &= \lambda_1 x_1 \\ Ax_2 &= \lambda_2 x_2 \end{align} \] Let \(x_1\) and \(x_2\) have any magnitude, so \(x_3\) can lie anywhere within their span: \[ x_3 = x_1 + x_2 \] What must be true about \(x_3\) if it is also an eigenvector? \[ Ax_3 = \lambda_3 x_3 \] We know that \(A x_3 = A x_1 + A x_2\) so we also know that: \[ \begin{align} \lambda_3 x_3 &= \lambda_1 x_1 + \lambda_2 x_2\\ \lambda_3 x_3 &= \lambda_3 x_1 + \lambda_3 x_2 \end{align} \] Clearly \(\lambda_1 = \lambda_2 = \lambda_3\). And if \(x_1\) and \(x_2\) are not linearly independent then \(\lambda_1 = \lambda_2\), since \(x_2\) must be a scalar multiple of \(x_1\). We will be interested in finding only new eigenvectors which lie outside the span of those already found, so that we can construct a basis to show more clearly that the transpose does not disturb the eigenvalues.

Next we will investigate a process called deflation, which will connect back to the power iterations and reveal the second eigenvector. The final challenge is to show that this process is identical to the second column of the QR algorithm.

I found this comment on Stack Exchange helpful:

As heads is tails 10/19

We know that
\( Ax = \lambda x \)
where \(x\) is the first eigenvector of A. But what is remarkable is that
\( A^\text{T}w = \lambda w \)
where \(w\) is the first eigenvector of \(A^\text{T}\). What is the meaning of this?

What is True 10/12

(Last Edit: 10/16/2025) \[ \begin{align} \alpha e_1 &= x - 2 u u^\text{T} x \\ [I - 2 u u^\text{T} ] \alpha e_1 &= x \\ \alpha e_1 - 2 \alpha u_1 u &= x \\ -2 \alpha u_1 u &= x - \alpha e_1 \\ c u &= x - \alpha e_1 \end{align} \] Because (says Copilot): \[ \begin{align} \left(I - 2uu^T\right)^T \left(I - 2uu^T\right) &= \left(I - 2uu^T\right)\left(I - 2uu^T\right) \\ &= I - 4uu^T + 4uu^T uu^T \\ &= I - 4uu^T + 4uu^T = I \end{align} \] If you need to normalize twice anyways you could do it this way, take the norm once to find \(\alpha\), then again to find \(u\). Now the singularity is avoided, but catastrophic cancelation (says copilot) can still wash out the vector if the subtraction is near zero, so you would still use sign flipping to increase stability. Could experiment with this more later. More importantly how do you find the second eigenvalue? It is possible to refactor multivariate polynomial equations into eigenvalue problems.


For Phoebus_V10:

def sign(x):
    return 1.0 if x >= 0 else -1.0

The solution is to guarantee that u0 = ph.sqrt((a-x[0])/(2*a)) will never be zero, and that this 2*a will not cause division by zero. The sign function in numpy returns 0 for np.sign(0) so that won't work. The sign function must be redefined as given above to always return a 1 or -1. Lastly a and x[0] can not be the same or this will produce a division by 0. So simply flipping the signs will work for all cases except where the norm of x is 0, in that case the entire column is 0 (this is a valid error condition). The last point suggested by Copilot is to normalize u again, rather than rely on the algebra. That might help with numerical stability in rare cases, however the sign flipping is a more fundamental design feature (Not just for numerical stability). So the norm will be computed twice, first to find a, then again to normalize u. This is good enough to move on to the second column.

import phoebus_V9 as ph

A = ph.array([[0,2,3],
              [1,2,1],
              [0,2,2]])

x = A[:,0] #first column of A

a = -ph.sign(x[0])*x.norm
u0 = ph.sqrt((a-x[0])/(2*a))

#reflection vector
u = -x/(2*a*u0)
u[0] = u0
u = u/u.norm

#construct the Householder reflection matrix
H = ph.eye(3) - 2*u*u.T

#Apply the reflection
H*A

The First Column 10/5

1. Power Iterations

1.1 \[ v_1 = \frac{A_1 e_1}{\| A_1 e_1 \|} \]
1.2 \[ v_2 = \frac{A_1 v_1}{\| A_1 v_1 \|} \]
1.K \[ v_k = \frac{A_1^k e_1}{\| A_1^k e_1 \|} \]
This process is very simple and converges on the first eigenvector for large k. This could be explored further later. Now the next process is the same thing.

2. QR Iterations

(where lowercase \(q_1\) denotes the first column of \(Q_1\)):

2.1 (Apply Definition 1) \[ A_1 = Q_1 R_1 \] \[ \begin{align} q_1 = \frac{a_1}{\| a_1 \|} &= \frac{A_1 e_1}{\|A_1 e_1\|} \\ v_1 &= q_1 = Q_1 e_1 \end{align} \] 2.2 (Apply Definition 1) This connection to the Power Iterations was explained to me by Copilot \[ A_2 = Q_1^\text{T} A_1 Q_1 = Q_2 R_2\] \[ \begin{align} q_2 = \frac{a_2}{\| a_2 \|} &= \frac{Q_1^\text{T} A_1 Q_1 e_1}{\|Q_1^\text{T} A_1 Q_1 e_1\|} \\ v_2 &= Q_1 q_2 = Q_1 Q_2 e_1 \end{align} \] 2.3 (Apply Definition 1) The pattern emerges: \[ A_3 = Q_2^\text{T} A_2 Q_2 = Q_3 R_3\] \[ \begin{align} q_3 = \frac{a_3}{\| a_3 \|} &= \frac{Q_2^\text{T}Q_1^\text{T} A_1 Q_1 Q_2 e_1}{\| Q_2^\text{T} Q_1^\text{T} A_1 Q_1 Q_2 e_1 \|} \\ v_3 &= Q_1 Q_2 q_3 = Q_1 Q_2 Q_3 e_1 \end{align} \] 3.K (Apply Definition 1) For the k'th iteration: \[ A_k = Q_{k-1}^\text{T} A_{k-1} Q_{k-1} = Q_k R_k\] \[ \begin{align} q_k = \frac{a_k}{\| a_k \|} &=\frac{Q_{k-1}^\text{T} \cdots Q_1^\text{T} A_1 Q_1 \cdots Q_{k-1} e_1}{\| Q_{k-1}^\text{T} \cdots Q_1^\text{T} A_1 Q_1 \cdots Q_{k-1} e_1 \|} \\ v_k &= Q_1 \cdots Q_{k-1} q_k = Q_1 \cdots Q_k e_1 \end{align}\] You can clearly see the k'th Power Iteration is constructed exactly if Definition 1 is true, which is standard QR with no sign flipping. To be looked into later; why in Householder QR the signs are flipped for stability in floating point systems? Likely not a lengthy diversion... So that will be this weeks topic before moving on to the next column. There are many such cases where the origin of a system does not obey the rules which apply to everyone else, so 0 has no multiplicative inverse, and the teachings of Jesus will lead you to life, except of course for Jesus himself, the paradox, his own teachings led him to death by crucifixion, but within the logical system of his teachings he is the origin, and so whether he is alive or dead is besides the point as well as \(\frac{0}{0}\) \[ v_k = \frac{A_1 v_{k-1}}{\| A_1 v_{k-1} \|} = \frac{A_1^k e_1}{\| A_1^k e_1 \|} \]

The Forest Through the Trees 10/2

Say you have a linear transformation
\(y = Ax\)

Now define some basis Q and express \(x\) and \(y\) in that new basis, you have:
\(Q y_Q = A Q x_Q \)

We can now say:
\(y_Q = Q^{-1} A Q x_Q \)


I am becoming worried that the weeds and the wild animals of calculus are the rainforest and linear algebra is the superhighway which is plowing down their home. Maybe it is because the destination is for the first time within reach, and there is time remaining. So I can take a diversion or two into the weeds. What was L'Hopital's rule all about, isn't it fascinating that you can evaluate \( \frac{0}{0} \) if \( \frac{ f(x) }{ g(x) } \) are both differentiable? Fascinating really, of course you can't divide by zero, but there in the middle of a fraction of polynomials or trig functions is a little origin point. I wonder if it is the same origin as the algebraic origin, the one where you say that every vector has a multiplicative inverse except for this one, this vector is the origin. Does it know the entire universe revolves around it?

9/29

Phoebus V9
We could start from scratch and rebuild the computer, but why waste time when we can already do #include < stdio.h > when we want to print something (printf), and #include < stdlib.h > when we want to convert a char array to an integer ( atoi(argv[1]) ). My computing 101 professor said to just memorize it! Did he waste my time? int main(int argc, char** argv) this isn't a whole lot and once memorized you don't need Copilot to slow you down. Now when considering QR, let's start with the first householder reflection:

import phoebus_V9 as ph

A = ph.array([[1,2,3],
              [3,2,1],
              [3,2,2]])

x = A[:,0] #first column of A

a = -ph.sign(x[0])*x.norm
u0 = ph.sqrt((a-x[0])/(2*a))

#reflection vector
u = -x/(2*a*u0)
u[0] = u0

#construct the Householder reflection matrix
H = ph.eye(3) - 2*u*u.T

#Apply the reflection
H*A

This gives us the first column of R in QR, to calculate eigenvalues with R*Q we need all the columns. Do this next, then circle back around and attack the power iterations.

9/23

Phoebus V7
What's going on is that in numpy you can't just do A[:,2] or it returns a 1d vector. But you can do:

import numpy as np

A = np.array([[1,2,3, 5, 6],
              [3,2,1, 5, 6],
              [3,2,2, 3, 3]])

A[:,slice(2,3)]

So this class indexes through the key and checks if it's an integer (isinstance(k, int)) and if so it replaces the integer with the slice operator which numpy recognizes. This works fine, now I can do Q_total[:,0] to select the first column without the unnecessary transpose. So, we're back in business. Now the question is why does this work:

import phoebus_V7 as ph

A = ph.array([[1,2,3],
              [3,2,1],
              [3,2,2]])

b = ph.array([1,0,0]).T

print("Power Iterations:")
for i in range(0,10):
    b = A*b
    b = b/b.norm #normalized eigenvector
    print(b.T)
    
s = b.T*A*b #largest eigenvalue
print(s)

A2 = A
Q_total = ph.eye(A.shape[0])

print("QR Iterations:")
for i in range(10):
    Q, R = A2.QR
    A2 = R * Q
    Q_total = Q_total * Q

    v = Q_total[:, 0]
    print(v.T)

s = v.T*A*v #largest eigenvalue
print(s)

Since we know that these two are equivalent, in the first QR decomposition we must simply be normalizing the first column of A. Likely that's the first step in QR decomposition, so the first task is implement QR factoring to gain an intuition of what that does, then return to the QR iterations and discover where the A*b step occurs in the second iteration. If QR simply normalizes the first column of R*Q then the first colum of R*Q must already contain A*b.
Copilot says that:
This isn't particularly helpful, but it seems to be the right direction to think of R*Q [:,0] as \(R q_1\) and then to find its connection with A. I should be able to implement QR with the phoebus module, Phoebus willing. Then move towards a clearer understanding of this all important mechanism.

9/14

Short on time so I had Copilot write the new array slicing function. Important enough not to vibe code this, so the new task is to understand this piece of code and simplify/improve it if possible. Then re-introduce the squeeze operator and test basic array broadcasting operations.

def __getitem__(self, key):
    print("Slicing with key:", key)

    # Normalize key to a tuple
    key = (key,) if not isinstance(key, tuple) else key

    # Convert integer indices to slices to preserve dimensions
    new_key = tuple(slice(k, k+1) if isinstance(k, int) else k for k in key)

    # Apply slicing
    sliced_data = self.data[new_key]

    # Wrap result in array class to preserve behavior
    return array(sliced_data)

9/07

(Phoebus Module V6) Didn't have time to fix up the array slicing, singleton dimensions should really be preserved by the array slicing operator, otherwise positional information is lost. (rows, cols, etc...) In Matlab the squeeze operator removes singleton dimensions. Just vibe coded the second part of this QR experiment and I am convinced that it works, at least it returns the same values as the power iterations. Now I know that the first column of the Q matrix does follow the same progression as the power iteration, but what's happening in the next column? Before moving on to that part, I need to figure out array slicing, then have Copilot explain why this works and what's happening in the second column. The official operating system of Point4D is Ubuntu Version 14. All core software will be written in C. Computers are not permitted to be connected to the internet. All personal cell phones and electronic equipment are checked at the security desk at the beginning of the work day. A programmer will have access to a guidebook which he will be expected to memorize. C will be the only language he will use.

import phoebus_V6 as ph

A = ph.array([[1,2,3],
              [3,2,1],
              [3,2,2]])

b = ph.array([1,0,0]).T

print("Power Iterations:")
for i in range(0,10):
    b = A*b
    b = b/b.norm #normalized eigenvector
    print(b.T)
    
s = b.T*A*b #largest eigenvalue
print(s)

A2 = A
Q_total = ph.eye(A.shape[0])

print("QR Iterations:")
for i in range(10):
    Q, R = A2.QR
    A2 = R * Q
    Q_total = Q_total * Q

    v = Q_total[:, 0].T
    print(v.T)

s = v.T*A*v #largest eigenvalue
print(s)

"Where no oxen are, the trough is clean" 8/31

Ubuntu Version 14 boots very fast, the login prompt contains a grid of evenly spaced points. Newer versions lost that grid, it was pretty cool. I was able to install Cuda version 8 and run some sample programs for a project at work on my old computer. When you think in 3D you say that using this equation I can predict the time at which a ball thrown in the air will hit the ground, when you think in 4D you say that the ball is a parabolic arc between two points, that the earth is a spiral in 4D... it is a shape, not a moving thing. Now looking at the power iteration, this is simple to understand. Multiplying by A a few times and normalizing takes you to the first eigenvalue. Clearly basis transformations won't disturb this eigenvalue, so you could just as easily start from R*Q and do the same iterations to find the first eigenvalue, but aparently you never even need the power iterations. You can just repeatedly R*Q. So the task is to find out where within the R*Q iterations does the power iteration live, at which point it should make sense. If I use the first column of Q as the initial guess for b can I trace those same values and reverse engineer this thing? In other words, if you were to ever understand how your own mind worked, then you would have two minds inside your own head, and there would be two of you not one.

import phoebus_V6 as ph

A = ph.array([[1,2,3],
              [3,2,1],
              [3,2,2]])


b = ph.rand((3,1)) #initial guess

for i in range(0,10):
    b = A*b

b = b/b.norm #normalized eigenvector
s = b.T*A*b #largest eigenvalue

One small step for Linear Algebra 8/24

(Phoebus Module V5) Two new features here. For one you can say A*3 or 3*A (thanks to Copilots suggestion to use __rmul__ to catch the 3*A case). Now something which always bugs me is when you're comparing matrices. I just want to say A==B and get true if the two matrices are equal. Now Phoebus V5 does that. I also added addition in the same way as scalar multiplication. As a simple test I'd like to test 4D affine transformations using this notation. Starting with deforming a sphere to create a phantom for ray-tracer testing. One gap in my knowledge is eigenvalues, could I use this notation to calculate eigenvalues? I might need a full QR for that, since QR iterations do R*Q each iteration. I guess you would need Q, so I'll add that and explore the QR algorithm further with this notation. How does it work? Start with the power iteration method for next weekend. How does that work? Can I use my new matrix class to find the first eigenvalue in a matrix? Finding eigenvalues is the foundation of SVD which is extremely usefull, so this is more important than a ray-tracer, but we'll get to that eventually. Add to the list, create a new page for just Phoebus updates. Then on this page complete the ray-tracer, although they are all related.

I installed Ubuntu 22.04.5 on an old computer this weekend. It runs great. The desktop actually works, and doesn't try and upload all my files to one drive. How nice. If I ever have time in this life to design an OS I would like folder layout to be like the old windows desktop but for folders too, so within each folder you can arrange icons like a desktop, and within each subfolder also another desktop. So you can arrange all your project files graphically and they will be in the same position each time you open the folder. Although it's a good start to simply have a functioning desktop with folders, something Windows can't say anymore. I suppose all the smart people at Microsoft have been working on Copilot integration.

import phoebus_V5 as ph

A = ph.array([[0,0,1],[0,1,1],[1,1,1],[1,1,0],[1,0,0]])
b = ph.array([.5,.7,1,.5,.3]).T

x = b >> A

print(A*x == b)
print(3*A + 1)

One giant leap for Python 8/17

(Phoebus Module V4)The basic notation is acceptable. Even refreshing after nearly a decade of Matlab. Next weekend I need to add support for scalar multiplication as well. For the case of A*3 for example... That aside we have proved that python can be made into a workable platform for linear algebra with the following example. See 4 methods of solving the same thing. b >> A solves the linear system with np.linalg.lstsqr or the standard least squares solution, but the notation really shines with factorizations.

In the naive case we break A into LU factors, and solve the new system with the >> operator. Since L is not square this will default to the least squares solver, and in a rather inefficient way. But you can always switch to the normal equations by multiplying A and b by A.T (the transpose) and take advantage of the >> optimization for square triangular matrices. Then the R only QR factoring of A allows the normal equations to be solved by substituting QR and letting the Q cancel out. When R is of full rank this will work, and the A.T*b >> R.T >> R is aesthetically pleasing and a fast triangular substitution.

This is starting to look like something I could write a ray-tracer in. I'm not sure if the ctypes library works with nvcc compiled code in the same way mex function in matlab can link cuda code for fast GPU acceleration. Further work, and a long journy of weekend projects ahead. We shall prevail with Apollo on our side and the Phoebus module will be the foundation of many great python programs. First for exploring reconstruction algorithms, then Physics simulation in general. An ambitious project but as President of Point4D I have instructed my entire technical team to focus on this project only. A clean syntax for linear algebra will pave the way for us to build our own LLM's and ultimately blow Nvidia out of the water. I would like to develop a platform for LLM's using this little chip GA144 which has a much cleaner architecture than a modern GPU although I would rather get my hands on one of Feinmans Connection Machines with 2^20 parallel computers (The vision was never realized). Likely sitting in a closet at the CIA or the FBI somewhere, (of course I wouldn't program it in "Lithp"). In 1987 they were measuring processor count in exponential notation while Nvidia is still advertising things like 24,064 CUDA Cores in a 10K $ chip. 2^20 is 1,048,576 cores. Going to need something like this to keep up with China in the AI arms race. I wouldn't bet on anything running on Nvidia.

import phoebus_V4 as ph

A = ph.array([[0,0,1],[0,1,1],[1,1,1],[1,1,0],[1,0,0]])
b = ph.array([.5,.7,1,.5,.3]).T

#Least squares solution
x = b >> A

#Naive Solve with LU
P, L, U = A.LU
x1 = P.T * b >> L >> U

#Solve Normal equations with LU
P, L, U = (A.T * A).LU
x2 = P.T * (A.T * b) >> L >> U

#Solve with R only substitution
R = A.R
x3 = A.T*b >> R.T >> R

The lesser evil 8/10

A new release: Phoebus Module V3 The focus here is on the triangular solver. For the rank deficient case we might as well fall back to lstqr, and since there is no way of knowing if a matrix is rank deficient without computing either SVD or QR, or trying LU it doesn't make sense to try one of the faster methods first. If you're going to fallback on lstqr anyways it's cleaner to just use that all the time. There might be some cases left to optimize, for example tall matrices where m>n I suspect it's faster to use QR, something like (R \ ( R' \ A'*b )) but since this library already supports triangular matrices, I just need to add a .R property and you could still do that with the triangular solver (if you knew R was full rank). Will test that next weekend.

import numpy as np
import phoebus_V3 as ps

A = ps.array([[1,2,3],[4,5,6],[4,5,6]])
b = ps.array([1,2,3]).T


P, L, U = A.LU
x_lu = P.T * b >> L >> U

x = b >> A

"Even gods Debug" 8/03

I will name my python module after Apollo, who killed Python with flaming arrows in an epic battle at the dawn of time. They say Python spread so far athwart the side of a vast mountain that it did strike fear into the hearts of man, as Ovid tells it. The Python slithered out of the slime that covered earth when the first flood receded. A child of the Suns rays, it is fitting that the sun god should kill it. (Phoebus Module V1) Phoebus is what the greeks called Apollo. Here is an example of the newly repurposed >> operator for solving linear systems. Now optimized for triangular matrices. Python transposes the permutation matrix in P,L,U = LU compared to Matlab. Both x_lu and x should return the same values, the later using np.linalg.solve for square systems or a least squares solution for non-square matrices. The operator checks if the system is triangular and selects forward/backward substitution if possible for speed. (Like Matlabs backslash) Probably a million ways you can crash this but as I get this tested I'll release new versions. I think np.linalg.solve will crash on underdetermined systems? Need to handle this case correctly. Working with MS Copilot on this project.

import numpy as np
import PhoebusV1 as mx

n = 10
A_np = np.random.rand(n, n)
b_np = np.random.rand(n)

A = mx.array(A_np)
b = mx.array(b_np).T

P, L, U = A.LU
x_lu = P.T * b >> L >> U

x = b >> A

Slaying the Serpent

Like god Apollo before me. Not optimized, would need checks for upper and lower triangular matrices and switch to triangular solver in those cases. But at least you can do x = P*b >> L >> U as a one liner. Redefining right shift, you would never need a binary shift operation on a matrix class anyways. This is workable.

import numpy as np
from scipy.linalg import lu

class Matrix:
    def __init__(self, data):
        self.data = np.array(data)

    def __mul__(self, other):
        result = np.matmul(self.data, other.data)
        return Matrix(result)

    def __rshift__(self, other):
        result = np.linalg.solve(other.data, self.data)
        return Matrix(result)

    def __getattr__(self, name):
        if name == 'T':
            return Matrix(self.data.T)
        elif name == 'LU':
            P, L, U = lu(self.data)
            return Matrix(P), Matrix(L), Matrix(U)

    def __repr__(self):
        return "Matrix(" + str(self.data.tolist()) + ")"


A = Matrix([[1,3,-2],[-5,2,1],[-2,-2,3]])
b = Matrix([1,2,3]).T

P, L, U = A.LU #LU factorization
x = P*b >> L >> U #solve system (not optimized)

Mass Attenuation Coefficients

Quick update to the previous method of sampling NIST tables. Should really be interpolating the points in log10 space, won't have a significant effect but the interpolated plots would have sharp discontinuities at the sample points. Just a matter of craftsmanship really.

Generated this plot in Octave, but switching to Python. (Joining the dark side?) The slower environment will force me to write more efficient code. The lack of elegant syntax for matrix multiplication is dissapointing, but is matrix multiplication necessary going forward? It's one of many operations which index over arrays, not everything is a matrix multiplication. Or maybe there is a way python can be extended.

Maybe MS Copilot has the answer:

import numpy as np

class Matrix:
    def __init__(self, data):
        self.data = np.array(data)

    def __mul__(self, other):
        result = np.matmul(self.data, other.data)
        return Matrix(result)

    def __repr__(self):
        return "Matrix(" + str(self.data.tolist() ) + ")"

A = Matrix([[1, 2], [3, 4]])
B = Matrix([[5, 6], [7, 8]])
C = A * B
print(C)

That's not bad, it lets you write A*B in python. I can customize this to add other operations too. Good enough for math. Numpy is fast enough, QT can do GUI's. But it's not pure enough for music, only Java will do. You could generalize this for AI operations. World is changing fast.

E = linspace(-3,log10(8),1000)'; %energy levels in log10 space
E = 10.^E;

%MU
M_tf = 0.240183*MU(6) + 0.759818*MU(9);
M_al = .969*MU(13)+.012*MU(12)+.008*MU(14)+.007*MU(26)+.004*MU(29);
M_st = .9908*MU(26) + .0075*MU(25) + .0017*MU(6);
M_ti = .90*MU(22) + .06*MU(13) + .04*MU(23);

figure
loglog(E, M_tf, 'DisplayName', 'Teflon');
hold on
loglog(E, M_al, 'DisplayName', 'Aluminum');
loglog(E, M_st, 'DisplayName', 'Steel');
loglog(E, M_ti, 'DisplayName', 'Titanium');

xlabel('Photon Energy [keV]', 'FontSize', 14)
ylabel('(\mu / \rho) [cm^2 /g]', 'FontSize', 14)
title('Mass Attenuation Coefficients', 'FontSize', 16)
legend show
set(gca, 'FontSize', 12)  % Enlarges tick labels

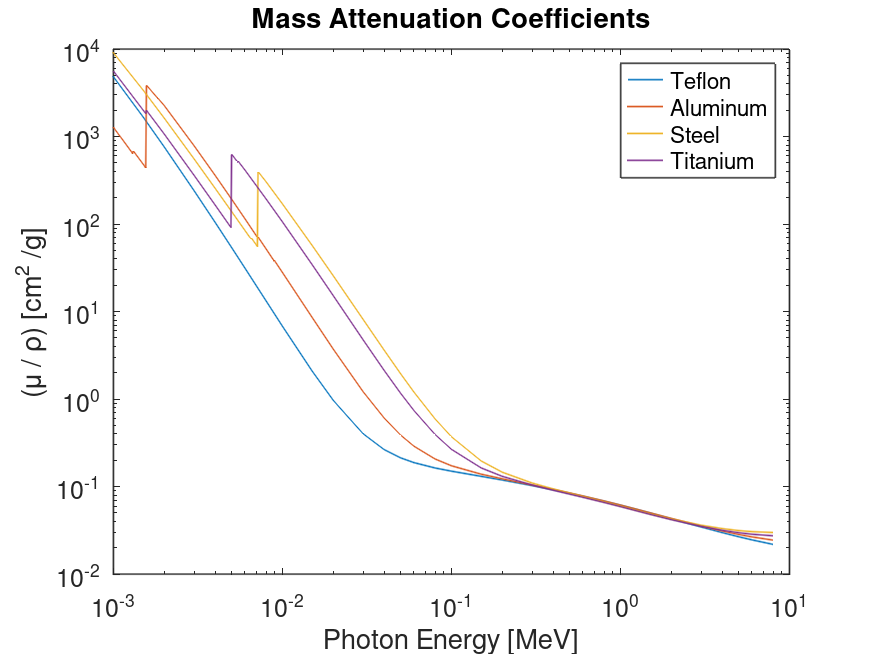
Figure 1

function mu1 = MU(i)
    %Source:
    %https://physics.nist.gov/PhysRefData/XrayMassCoef/tab3.html
    mu_cell = {
    [7.217e+00, 2.148e+00, 1.059e+00, 5.612e-01, 4.546e-01, 4.193e-01, 4.042e-01, 3.914e-01, 3.854e-01, 3.764e-01, 3.695e-01, 3.570e-01, 3.458e-01, 3.355e-01, 3.260e-01, 3.091e-01, 2.944e-01, 2.651e-01, 2.429e-01, 2.112e-01, 1.893e-01, 1.729e-01, 1.599e-01, 1.405e-01, 1.263e-01, 1.129e-01, 1.027e-01, 8.769e-02, 6.921e-02, 5.806e-02, 5.049e-02, 4.498e-02, 3.746e-02, 3.254e-02, 2.539e-02, 2.153e-02]
    [6.084e+01, 1.676e+01, 6.863e+00, 2.007e+00, 9.329e-01, 5.766e-01, 4.195e-01, 2.933e-01, 2.476e-01, 2.092e-01, 1.960e-01, 1.838e-01, 1.763e-01, 1.703e-01, 1.651e-01, 1.562e-01, 1.486e-01, 1.336e-01, 1.224e-01, 1.064e-01, 9.535e-02, 8.707e-02, 8.054e-02, 7.076e-02, 6.362e-02, 5.688e-02, 5.173e-02, 4.422e-02, 3.503e-02, 2.949e-02, 2.577e-02, 2.307e-02, 1.940e-02, 1.703e-02, 1.363e-02, 1.183e-02]
    [2.339e+02, 6.668e+01, 2.707e+01, 7.549e+00, 3.114e+00, 1.619e+00, 9.875e-01, 5.054e-01, 3.395e-01, 2.176e-01, 1.856e-01, 1.644e-01, 1.551e-01, 1.488e-01, 1.438e-01, 1.356e-01, 1.289e-01, 1.158e-01, 1.060e-01, 9.210e-02, 8.249e-02, 7.532e-02, 6.968e-02, 6.121e-02, 5.503e-02, 4.921e-02, 4.476e-02, 3.830e-02, 3.043e-02, 2.572e-02, 2.257e-02, 2.030e-02, 1.725e-02, 1.529e-02, 1.252e-02, 1.109e-02]
    [6.041e+02, 1.797e+02, 7.469e+01, 2.127e+01, 8.685e+00, 4.369e+00, 2.527e+00, 1.124e+00, 6.466e-01, 3.070e-01, 2.251e-01, 1.792e-01, 1.640e-01, 1.554e-01, 1.493e-01, 1.401e-01, 1.328e-01, 1.190e-01, 1.089e-01, 9.463e-02, 8.471e-02, 7.739e-02, 7.155e-02, 6.286e-02, 5.652e-02, 5.054e-02, 4.597e-02, 3.938e-02, 3.138e-02, 2.664e-02, 2.347e-02, 2.121e-02, 1.819e-02, 1.627e-02, 1.361e-02, 1.227e-02]
    [1.229e+03, 3.766e+02, 1.597e+02, 4.667e+01, 1.927e+01, 9.683e+00, 5.538e+00, 2.346e+00, 1.255e+00, 4.827e-01, 3.014e-01, 2.063e-01, 1.793e-01, 1.665e-01, 1.583e-01, 1.472e-01, 1.391e-01, 1.243e-01, 1.136e-01, 9.862e-02, 8.834e-02, 8.065e-02, 7.460e-02, 6.549e-02, 5.890e-02, 5.266e-02, 4.791e-02, 4.108e-02, 3.284e-02, 2.798e-02, 2.476e-02, 2.248e-02, 1.945e-02, 1.755e-02, 1.495e-02, 1.368e-02]
    [2.211e+03, 7.002e+02, 3.026e+02, 9.033e+01, 3.778e+01, 1.912e+01, 1.095e+01, 4.576e+00, 2.373e+00, 8.071e-01, 4.420e-01, 2.562e-01, 2.076e-01, 1.871e-01, 1.753e-01, 1.610e-01, 1.514e-01, 1.347e-01, 1.229e-01, 1.066e-01, 9.546e-02, 8.715e-02, 8.058e-02, 7.076e-02, 6.361e-02, 5.690e-02, 5.179e-02, 4.442e-02, 3.562e-02, 3.047e-02, 2.708e-02, 2.469e-02, 2.154e-02, 1.959e-02, 1.698e-02, 1.575e-02]
    [3.311e+03, 1.083e+03, 4.769e+02, 1.456e+02, 6.166e+01, 3.144e+01, 1.809e+01, 7.562e+00, 3.879e+00, 1.236e+00, 6.178e-01, 3.066e-01, 2.288e-01, 1.980e-01, 1.817e-01, 1.639e-01, 1.529e-01, 1.353e-01, 1.233e-01, 1.068e-01, 9.557e-02, 8.719e-02, 8.063e-02, 7.081e-02, 6.364e-02, 5.693e-02, 5.180e-02, 4.450e-02, 3.579e-02, 3.073e-02, 2.742e-02, 2.511e-02, 2.209e-02, 2.024e-02, 1.782e-02, 1.673e-02]
    [4.590e+03, 1.549e+03, 6.949e+02, 2.171e+02, 9.315e+01, 4.790e+01, 2.770e+01, 1.163e+01, 5.952e+00, 1.836e+00, 8.651e-01, 3.779e-01, 2.585e-01, 2.132e-01, 1.907e-01, 1.678e-01, 1.551e-01, 1.361e-01, 1.237e-01, 1.070e-01, 9.566e-02, 8.729e-02, 8.070e-02, 7.087e-02, 6.372e-02, 5.697e-02, 5.185e-02, 4.459e-02, 3.597e-02, 3.100e-02, 2.777e-02, 2.552e-02, 2.263e-02, 2.089e-02, 1.866e-02, 1.770e-02]
    [5.649e+03, 1.979e+03, 9.047e+02, 2.888e+02, 1.256e+02, 6.514e+01, 3.789e+01, 1.602e+01, 8.205e+00, 2.492e+00, 1.133e+00, 4.487e-01, 2.828e-01, 2.214e-01, 1.920e-01, 1.639e-01, 1.496e-01, 1.298e-01, 1.176e-01, 1.015e-01, 9.073e-02, 8.274e-02, 7.649e-02, 6.717e-02, 6.037e-02, 5.399e-02, 4.915e-02, 4.228e-02, 3.422e-02, 2.960e-02, 2.663e-02, 2.457e-02, 2.195e-02, 2.039e-02, 1.846e-02, 1.769e-02]
    [7.409e+03, 2.666e+03, 1.243e+03, 4.051e+02, 1.785e+02, 9.339e+01, 5.467e+01, 2.328e+01, 1.197e+01, 3.613e+00, 1.606e+00, 5.923e-01, 3.473e-01, 2.579e-01, 2.161e-01, 1.781e-01, 1.600e-01, 1.370e-01, 1.236e-01, 1.064e-01, 9.502e-02, 8.664e-02, 8.006e-02, 7.029e-02, 6.316e-02, 5.646e-02, 5.145e-02, 4.430e-02, 3.594e-02, 3.122e-02, 2.818e-02, 2.610e-02, 2.348e-02, 2.197e-02, 2.013e-02, 1.946e-02]
    [6.542e+02, 5.960e+02, 5.429e+02, 6.435e+03, 3.194e+03, 1.521e+03, 5.070e+02, 2.261e+02, 1.194e+02, 7.030e+01, 3.018e+01, 1.557e+01, 4.694e+00, 2.057e+00, 7.197e-01, 3.969e-01, 2.804e-01, 2.268e-01, 1.796e-01, 1.585e-01, 1.335e-01, 1.199e-01, 1.029e-01, 9.185e-02, 8.372e-02, 7.736e-02, 6.788e-02, 6.100e-02, 5.454e-02, 4.968e-02, 4.282e-02, 3.487e-02, 3.037e-02, 2.753e-02, 2.559e-02, 2.319e-02, 2.181e-02, 2.023e-02, 1.970e-02]
    [9.225e+02, 6.474e+02, 4.530e+02, 5.444e+03, 4.004e+03, 1.932e+03, 6.585e+02, 2.974e+02, 1.583e+02, 9.381e+01, 4.061e+01, 2.105e+01, 6.358e+00, 2.763e+00, 9.306e-01, 4.881e-01, 3.292e-01, 2.570e-01, 1.951e-01, 1.686e-01, 1.394e-01, 1.245e-01, 1.065e-01, 9.492e-02, 8.647e-02, 7.988e-02, 7.008e-02, 6.296e-02, 5.629e-02, 5.129e-02, 4.426e-02, 3.613e-02, 3.159e-02, 2.873e-02, 2.681e-02, 2.445e-02, 2.313e-02, 2.168e-02, 2.127e-02]
    [1.185e+03, 4.022e+02, 3.621e+02, 3.957e+03, 2.263e+03, 7.880e+02, 3.605e+02, 1.934e+02, 1.153e+02, 5.033e+01, 2.623e+01, 7.955e+00, 3.441e+00, 1.128e+00, 5.685e-01, 3.681e-01, 2.778e-01, 2.018e-01, 1.704e-01, 1.378e-01, 1.223e-01, 1.042e-01, 9.276e-02, 8.445e-02, 7.802e-02, 6.841e-02, 6.146e-02, 5.496e-02, 5.006e-02, 4.324e-02, 3.541e-02, 3.106e-02, 2.836e-02, 2.655e-02, 2.437e-02, 2.318e-02, 2.195e-02, 2.168e-02]
    [1.570e+03, 5.355e+02, 3.092e+02, 3.192e+03, 2.777e+03, 9.784e+02, 4.529e+02, 2.450e+02, 1.470e+02, 6.468e+01, 3.389e+01, 1.034e+01, 4.464e+00, 1.436e+00, 7.012e-01, 4.385e-01, 3.207e-01, 2.228e-01, 1.835e-01, 1.448e-01, 1.275e-01, 1.082e-01, 9.614e-02, 8.748e-02, 8.077e-02, 7.082e-02, 6.361e-02, 5.688e-02, 5.183e-02, 4.480e-02, 3.678e-02, 3.240e-02, 2.967e-02, 2.788e-02, 2.574e-02, 2.462e-02, 2.352e-02, 2.338e-02]
    [1.913e+03, 6.547e+02, 3.018e+02, 2.494e+02, 2.473e+03, 1.118e+03, 5.242e+02, 2.860e+02, 1.726e+02, 7.660e+01, 4.035e+01, 1.239e+01, 5.352e+00, 1.700e+00, 8.096e-01, 4.916e-01, 3.494e-01, 2.324e-01, 1.865e-01, 1.432e-01, 1.250e-01, 1.055e-01, 9.359e-02, 8.511e-02, 7.854e-02, 6.884e-02, 6.182e-02, 5.526e-02, 5.039e-02, 4.358e-02, 3.590e-02, 3.172e-02, 2.915e-02, 2.747e-02, 2.552e-02, 2.452e-02, 2.364e-02, 2.363e-02]
    [2.429e+03, 8.342e+02, 3.853e+02, 2.168e+02, 2.070e+03, 1.339e+03, 6.338e+02, 3.487e+02, 2.116e+02, 9.465e+01, 5.012e+01, 1.550e+01, 6.708e+00, 2.113e+00, 9.872e-01, 5.849e-01, 4.053e-01, 2.585e-01, 2.020e-01, 1.506e-01, 1.302e-01, 1.091e-01, 9.665e-02, 8.781e-02, 8.102e-02, 7.098e-02, 6.373e-02, 5.697e-02, 5.193e-02, 4.498e-02, 3.715e-02, 3.293e-02, 3.036e-02, 2.872e-02, 2.682e-02, 2.589e-02, 2.517e-02, 2.529e-02]
    [2.832e+03, 9.771e+02, 4.520e+02, 1.774e+02, 1.637e+03, 1.473e+03, 7.037e+02, 3.901e+02, 2.384e+02, 1.075e+02, 5.725e+01, 1.784e+01, 7.739e+00, 2.425e+00, 1.117e+00, 6.483e-01, 4.395e-01, 2.696e-01, 2.050e-01, 1.480e-01, 1.266e-01, 1.054e-01, 9.311e-02, 8.453e-02, 7.795e-02, 6.826e-02, 6.128e-02, 5.478e-02, 4.994e-02, 4.328e-02, 3.585e-02, 3.188e-02, 2.950e-02, 2.798e-02, 2.628e-02, 2.549e-02, 2.496e-02, 2.520e-02]
    [3.184e+03, 1.105e+03, 5.120e+02, 1.703e+02, 1.424e+02, 1.275e+03, 7.572e+02, 4.225e+02, 2.593e+02, 1.180e+02, 6.316e+01, 1.983e+01, 8.629e+00, 2.697e+00, 1.228e+00, 7.012e-01, 4.664e-01, 2.760e-01, 2.043e-01, 1.427e-01, 1.205e-01, 9.953e-02, 8.776e-02, 7.958e-02, 7.335e-02, 6.419e-02, 5.762e-02, 5.150e-02, 4.695e-02, 4.074e-02, 3.384e-02, 3.019e-02, 2.802e-02, 2.667e-02, 2.517e-02, 2.451e-02, 2.418e-02, 2.453e-02]
    [4.058e+03, 1.418e+03, 6.592e+02, 2.198e+02, 1.327e+02, 1.201e+03, 9.256e+02, 5.189e+02, 3.205e+02, 1.469e+02, 7.907e+01, 2.503e+01, 1.093e+01, 3.413e+00, 1.541e+00, 8.679e-01, 5.678e-01, 3.251e-01, 2.345e-01, 1.582e-01, 1.319e-01, 1.080e-01, 9.495e-02, 8.600e-02, 7.922e-02, 6.929e-02, 6.216e-02, 5.556e-02, 5.068e-02, 4.399e-02, 3.666e-02, 3.282e-02, 3.054e-02, 2.915e-02, 2.766e-02, 2.704e-02, 2.687e-02, 2.737e-02]
    [4.867e+03, 1.714e+03, 7.999e+02, 2.676e+02, 1.218e+02, 1.187e+02, 1.023e+03, 6.026e+02, 3.731e+02, 1.726e+02, 9.341e+01, 2.979e+01, 1.306e+01, 4.080e+00, 1.830e+00, 1.019e+00, 6.578e-01, 3.656e-01, 2.571e-01, 1.674e-01, 1.376e-01, 1.116e-01, 9.783e-02, 8.851e-02, 8.148e-02, 7.122e-02, 6.388e-02, 5.709e-02, 5.207e-02, 4.524e-02, 3.780e-02, 3.395e-02, 3.170e-02, 3.035e-02, 2.892e-02, 2.839e-02, 2.838e-02, 2.903e-02]
    [5.238e+03, 1.858e+03, 8.706e+02, 2.922e+02, 1.332e+02, 9.687e+01, 8.148e+02, 6.305e+02, 3.933e+02, 1.828e+02, 9.952e+01, 3.202e+01, 1.409e+01, 4.409e+00, 1.969e+00, 1.087e+00, 6.932e-01, 3.753e-01, 2.577e-01, 1.619e-01, 1.310e-01, 1.052e-01, 9.193e-02, 8.305e-02, 7.639e-02, 6.675e-02, 5.985e-02, 5.347e-02, 4.878e-02, 4.243e-02, 3.554e-02, 3.202e-02, 2.999e-02, 2.878e-02, 2.756e-02, 2.715e-02, 2.732e-02, 2.804e-02]
    [5.869e+03, 2.096e+03, 9.860e+02, 3.323e+02, 1.517e+02, 8.380e+01, 6.878e+02, 6.838e+02, 4.323e+02, 2.023e+02, 1.107e+02, 3.587e+01, 1.585e+01, 4.972e+00, 2.214e+00, 1.213e+00, 7.661e-01, 4.052e-01, 2.721e-01, 1.649e-01, 1.314e-01, 1.043e-01, 9.081e-02, 8.191e-02, 7.529e-02, 6.572e-02, 5.891e-02, 5.263e-02, 4.801e-02, 4.180e-02, 3.512e-02, 3.173e-02, 2.982e-02, 2.868e-02, 2.759e-02, 2.727e-02, 2.762e-02, 2.844e-02]
    [6.495e+03, 2.342e+03, 1.106e+03, 3.743e+02, 1.712e+02, 9.291e+01, 7.277e+01, 5.870e+02, 4.687e+02, 2.217e+02, 1.218e+02, 3.983e+01, 1.768e+01, 5.564e+00, 2.472e+00, 1.347e+00, 8.438e-01, 4.371e-01, 2.877e-01, 1.682e-01, 1.318e-01, 1.034e-01, 8.965e-02, 8.074e-02, 7.414e-02, 6.466e-02, 5.794e-02, 5.175e-02, 4.722e-02, 4.115e-02, 3.466e-02, 3.141e-02, 2.960e-02, 2.855e-02, 2.759e-02, 2.738e-02, 2.786e-02, 2.877e-02]
    [7.405e+03, 2.694e+03, 1.277e+03, 4.339e+02, 1.988e+02, 1.080e+02, 6.574e+01, 5.977e+02, 5.160e+02, 2.513e+02, 1.386e+02, 4.571e+01, 2.038e+01, 6.434e+00, 2.856e+00, 1.550e+00, 9.639e-01, 4.905e-01, 3.166e-01, 1.788e-01, 1.378e-01, 1.067e-01, 9.213e-02, 8.281e-02, 7.598e-02, 6.620e-02, 5.930e-02, 5.295e-02, 4.832e-02, 4.213e-02, 3.559e-02, 3.235e-02, 3.057e-02, 2.956e-02, 2.869e-02, 2.855e-02, 2.920e-02, 3.026e-02]
    [8.093e+03, 2.984e+03, 1.421e+03, 4.851e+02, 2.229e+02, 1.212e+02, 7.350e+01, 5.803e+01, 4.520e+02, 2.734e+02, 1.514e+02, 5.027e+01, 2.253e+01, 7.141e+00, 3.169e+00, 1.714e+00, 1.060e+00, 5.306e-01, 3.367e-01, 1.838e-01, 1.391e-01, 1.062e-01, 9.133e-02, 8.192e-02, 7.509e-02, 6.537e-02, 5.852e-02, 5.224e-02, 4.769e-02, 4.162e-02, 3.524e-02, 3.213e-02, 3.045e-02, 2.952e-02, 2.875e-02, 2.871e-02, 2.951e-02, 3.068e-02]
    [9.085e+03, 3.399e+03, 1.626e+03, 5.576e+02, 2.567e+02, 1.398e+02, 8.484e+01, 5.319e+01, 4.076e+02, 3.056e+02, 1.706e+02, 5.708e+01, 2.568e+01, 8.176e+00, 3.629e+00, 1.958e+00, 1.205e+00, 5.952e-01, 3.717e-01, 1.964e-01, 1.460e-01, 1.099e-01, 9.400e-02, 8.414e-02, 7.704e-02, 6.699e-02, 5.995e-02, 5.350e-02, 4.883e-02, 4.265e-02, 3.621e-02, 3.312e-02, 3.146e-02, 3.057e-02, 2.991e-02, 2.994e-02, 3.092e-02, 3.224e-02]
    [9.796e+03, 3.697e+03, 1.779e+03, 6.129e+02, 2.830e+02, 1.543e+02, 9.370e+01, 4.710e+01, 3.555e+02, 3.248e+02, 1.841e+02, 6.201e+01, 2.803e+01, 8.962e+00, 3.981e+00, 2.144e+00, 1.314e+00, 6.414e-01, 3.949e-01, 2.023e-01, 1.476e-01, 1.094e-01, 9.311e-02, 8.315e-02, 7.604e-02, 6.604e-02, 5.906e-02, 5.270e-02, 4.810e-02, 4.204e-02, 3.580e-02, 3.283e-02, 3.127e-02, 3.045e-02, 2.991e-02, 3.002e-02, 3.115e-02, 3.256e-02]
    [9.855e+03, 9.753e+03, 9.654e+03, 1.099e+04, 4.234e+03, 2.049e+03, 7.094e+02, 3.282e+02, 1.793e+02, 1.090e+02, 4.952e+01, 4.428e+01, 3.294e+02, 2.090e+02, 7.081e+01, 3.220e+01, 1.034e+01, 4.600e+00, 2.474e+00, 1.512e+00, 7.306e-01, 4.440e-01, 2.208e-01, 1.582e-01, 1.154e-01, 9.765e-02, 8.698e-02, 7.944e-02, 6.891e-02, 6.160e-02, 5.494e-02, 5.015e-02, 4.387e-02, 3.745e-02, 3.444e-02, 3.289e-02, 3.210e-02, 3.164e-02, 3.185e-02, 3.320e-02, 3.476e-02]
    [1.057e+04, 9.307e+03, 8.242e+03, 9.347e+03, 4.418e+03, 2.154e+03, 7.488e+02, 3.473e+02, 1.899e+02, 1.156e+02, 5.255e+01, 3.829e+01, 2.784e+02, 2.159e+02, 7.405e+01, 3.379e+01, 1.092e+01, 4.862e+00, 2.613e+00, 1.593e+00, 7.630e-01, 4.584e-01, 2.217e-01, 1.559e-01, 1.119e-01, 9.413e-02, 8.362e-02, 7.625e-02, 6.605e-02, 5.901e-02, 5.261e-02, 4.803e-02, 4.205e-02, 3.599e-02, 3.318e-02, 3.177e-02, 3.108e-02, 3.074e-02, 3.103e-02, 3.247e-02, 3.408e-02]
    [1.553e+03, 1.518e+03, 1.484e+03, 3.804e+03, 5.097e+03, 6.518e+03, 8.274e+03, 8.452e+03, 7.371e+03, 8.396e+03, 4.825e+03, 2.375e+03, 8.311e+02, 3.865e+02, 2.118e+02, 1.290e+02, 5.875e+01, 3.505e+01, 2.536e+02, 2.331e+02, 8.117e+01, 3.719e+01, 1.207e+01, 5.384e+00, 2.892e+00, 1.760e+00, 8.364e-01, 4.973e-01, 2.341e-01, 1.617e-01, 1.141e-01, 9.539e-02, 8.450e-02, 7.695e-02, 6.656e-02, 5.941e-02, 5.296e-02, 4.834e-02, 4.235e-02, 3.634e-02, 3.360e-02, 3.225e-02, 3.160e-02, 3.138e-02, 3.175e-02, 3.335e-02, 3.509e-02]
    [1.697e+03, 1.492e+03, 1.312e+03, 3.990e+03, 4.887e+03, 5.664e+03, 7.405e+03, 7.138e+03, 6.358e+03, 7.206e+03, 5.087e+03, 2.515e+03, 8.857e+02, 4.130e+02, 2.266e+02, 1.382e+02, 6.302e+01, 3.421e+01, 3.099e+01, 2.214e+02, 8.537e+01, 3.928e+01, 1.281e+01, 5.726e+00, 3.076e+00, 1.868e+00, 8.823e-01, 5.197e-01, 2.387e-01, 1.619e-01, 1.123e-01, 9.325e-02, 8.236e-02, 7.487e-02, 6.466e-02, 5.767e-02, 5.139e-02, 4.692e-02, 4.113e-02, 3.538e-02, 3.280e-02, 3.156e-02, 3.099e-02, 3.086e-02, 3.130e-02, 3.300e-02, 3.479e-02]
    [1.893e+03, 1.502e+03, 1.190e+03, 4.389e+03, 4.734e+03, 4.974e+03, 6.698e+03, 6.348e+03, 5.554e+03, 6.287e+03, 5.475e+03, 2.711e+03, 9.613e+02, 4.497e+02, 2.472e+02, 1.509e+02, 6.890e+01, 3.742e+01, 2.811e+01, 1.981e+02, 9.152e+01, 4.222e+01, 1.385e+01, 6.207e+00, 3.335e+00, 2.023e+00, 9.501e-01, 5.550e-01, 2.491e-01, 1.661e-01, 1.131e-01, 9.327e-02, 8.212e-02, 7.452e-02, 6.426e-02, 5.727e-02, 5.101e-02, 4.657e-02, 4.086e-02, 3.524e-02, 3.275e-02, 3.158e-02, 3.107e-02, 3.103e-02, 3.156e-02, 3.340e-02, 3.528e-02]
    [2.121e+03, 1.523e+03, 1.092e+03, 4.513e+03, 4.469e+03, 4.452e+03, 6.093e+03, 5.227e+03, 4.997e+03, 5.653e+03, 2.931e+03, 1.049e+03, 4.920e+02, 2.709e+02, 1.656e+02, 7.573e+01, 4.115e+01, 2.577e+01, 1.792e+02, 9.856e+01, 4.564e+01, 1.506e+01, 6.760e+00, 3.635e+00, 2.203e+00, 1.030e+00, 5.971e-01, 2.622e-01, 1.719e-01, 1.150e-01, 9.414e-02, 8.259e-02, 7.483e-02, 6.440e-02, 5.735e-02, 5.106e-02, 4.661e-02, 4.093e-02, 3.539e-02, 3.296e-02, 3.187e-02, 3.141e-02, 3.146e-02, 3.207e-02, 3.405e-02, 3.603e-02]
    [2.317e+03, 1.512e+03, 9.814e+02, 4.347e+03, 4.057e+03, 3.907e+03, 5.186e+03, 5.336e+03, 4.342e+03, 4.915e+03, 3.098e+03, 1.116e+03, 5.252e+02, 2.896e+02, 1.773e+02, 8.116e+01, 4.414e+01, 2.318e+01, 1.589e+02, 1.033e+02, 4.818e+01, 1.596e+01, 7.184e+00, 3.864e+00, 2.341e+00, 1.090e+00, 6.278e-01, 2.703e-01, 1.742e-01, 1.144e-01, 9.299e-02, 8.129e-02, 7.350e-02, 6.314e-02, 5.619e-02, 4.999e-02, 4.564e-02, 4.010e-02, 3.476e-02, 3.247e-02, 3.145e-02, 3.105e-02, 3.119e-02, 3.186e-02, 3.395e-02, 3.599e-02]
    [2.624e+03, 1.002e+03, 9.255e+02, 4.289e+03, 3.838e+03, 3.587e+03, 5.097e+03, 4.595e+03, 3.969e+03, 4.495e+03, 3.407e+03, 1.231e+03, 5.815e+02, 3.213e+02, 1.968e+02, 9.026e+01, 4.912e+01, 2.176e+01, 1.471e+02, 1.119e+02, 5.266e+01, 1.753e+01, 7.900e+00, 4.264e+00, 2.582e+00, 1.198e+00, 6.861e-01, 2.899e-01, 1.838e-01, 1.186e-01, 9.563e-02, 8.328e-02, 7.515e-02, 6.443e-02, 5.728e-02, 5.094e-02, 4.650e-02, 4.089e-02, 3.552e-02, 3.327e-02, 3.229e-02, 3.194e-02, 3.218e-02, 3.293e-02, 3.521e-02, 3.738e-02]
    [2.854e+03, 1.093e+03, 8.361e+02, 3.909e+03, 3.409e+03, 3.166e+03, 4.566e+03, 4.014e+03, 3.482e+03, 3.948e+03, 3.599e+03, 1.305e+03, 6.186e+02, 3.425e+02, 2.101e+02, 9.651e+01, 5.257e+01, 1.971e+01, 1.313e+02, 1.168e+02, 5.548e+01, 1.854e+01, 8.389e+00, 4.523e+00, 2.739e+00, 1.267e+00, 7.221e-01, 2.998e-01, 1.872e-01, 1.186e-01, 9.480e-02, 8.226e-02, 7.410e-02, 6.340e-02, 5.631e-02, 5.005e-02, 4.569e-02, 4.020e-02, 3.501e-02, 3.286e-02, 3.196e-02, 3.168e-02, 3.199e-02, 3.280e-02, 3.518e-02, 3.741e-02]
    [3.174e+03, 1.219e+03, 7.782e+02, 3.096e+03, 2.969e+03, 2.861e+03, 3.957e+03, 3.410e+03, 3.153e+03, 3.606e+03, 1.418e+03, 6.748e+02, 3.744e+02, 2.300e+02, 1.058e+02, 5.766e+01, 1.909e+01, 1.842e+01, 1.208e+02, 5.980e+01, 2.009e+01, 9.112e+00, 4.918e+00, 2.979e+00, 1.375e+00, 7.799e-01, 3.187e-01, 1.960e-01, 1.219e-01, 9.670e-02, 8.360e-02, 7.510e-02, 6.412e-02, 5.689e-02, 5.053e-02, 4.613e-02, 4.061e-02, 3.545e-02, 3.335e-02, 3.250e-02, 3.227e-02, 3.267e-02, 3.357e-02, 3.610e-02, 3.845e-02]
    [3.494e+03, 1.347e+03, 7.207e+02, 2.864e+03, 2.589e+03, 2.571e+03, 3.577e+03, 3.201e+03, 2.842e+03, 3.241e+03, 1.525e+03, 7.297e+02, 4.058e+02, 2.496e+02, 1.150e+02, 6.274e+01, 2.079e+01, 1.714e+01, 1.108e+02, 6.386e+01, 2.157e+01, 9.818e+00, 5.306e+00, 3.214e+00, 1.481e+00, 8.365e-01, 3.369e-01, 2.042e-01, 1.247e-01, 9.811e-02, 8.443e-02, 7.570e-02, 6.447e-02, 5.714e-02, 5.072e-02, 4.630e-02, 4.079e-02, 3.569e-02, 3.365e-02, 3.286e-02, 3.268e-02, 3.317e-02, 3.414e-02, 3.683e-02, 3.927e-02]
    [3.864e+03, 1.493e+03, 7.422e+02, 6.738e+02, 2.627e+03, 2.466e+03, 2.342e+03, 3.264e+03, 2.916e+03, 2.597e+03, 2.962e+03, 1.654e+03, 7.936e+02, 4.424e+02, 2.725e+02, 1.258e+02, 6.871e+01, 2.279e+01, 1.612e+01, 1.029e+02, 6.855e+01, 2.330e+01, 1.065e+01, 5.764e+00, 3.493e+00, 1.607e+00, 9.047e-01, 3.595e-01, 2.149e-01, 1.289e-01, 1.006e-01, 8.613e-02, 7.703e-02, 6.546e-02, 5.795e-02, 5.141e-02, 4.692e-02, 4.137e-02, 3.628e-02, 3.428e-02, 3.355e-02, 3.341e-02, 3.399e-02, 3.504e-02, 3.790e-02, 4.048e-02]
    [4.210e+03, 1.631e+03, 8.115e+02, 6.258e+02, 2.392e+03, 2.239e+03, 2.120e+03, 2.953e+03, 2.641e+03, 2.359e+03, 2.691e+03, 1.772e+03, 8.507e+02, 4.755e+02, 2.935e+02, 1.356e+02, 7.417e+01, 2.463e+01, 1.501e+01, 9.470e+01, 7.237e+01, 2.485e+01, 1.139e+01, 6.173e+00, 3.744e+00, 1.721e+00, 9.658e-01, 3.790e-01, 2.237e-01, 1.318e-01, 1.018e-01, 8.693e-02, 7.756e-02, 6.571e-02, 5.810e-02, 5.150e-02, 4.700e-02, 4.146e-02, 3.644e-02, 3.451e-02, 3.384e-02, 3.374e-02, 3.441e-02, 3.554e-02, 3.855e-02, 4.122e-02]
    [4.600e+03, 1.786e+03, 8.893e+02, 5.844e+02, 2.181e+03, 2.045e+03, 1.935e+03, 2.694e+03, 2.412e+03, 2.161e+03, 2.470e+03, 1.906e+03, 9.164e+02, 5.134e+02, 3.172e+02, 1.469e+02, 8.038e+01, 2.672e+01, 1.409e+01, 8.784e+01, 7.712e+01, 2.666e+01, 1.223e+01, 6.644e+00, 4.032e+00, 1.852e+00, 1.037e+00, 4.023e-01, 2.344e-01, 1.357e-01, 1.040e-01, 8.831e-02, 7.858e-02, 6.642e-02, 5.866e-02, 5.196e-02, 4.741e-02, 4.185e-02, 3.686e-02, 3.498e-02, 3.436e-02, 3.432e-02, 3.508e-02, 3.628e-02, 3.944e-02, 4.224e-02]
    [4.942e+03, 1.925e+03, 9.593e+02, 5.415e+02, 1.979e+03, 1.854e+03, 1.750e+03, 2.433e+03, 2.183e+03, 1.961e+03, 2.243e+03, 2.011e+03, 9.703e+02, 5.450e+02, 3.373e+02, 1.565e+02, 8.576e+01, 2.854e+01, 1.308e+01, 8.055e+01, 8.054e+01, 2.810e+01, 1.294e+01, 7.037e+00, 4.274e+00, 1.962e+00, 1.096e+00, 4.208e-01, 2.423e-01, 1.379e-01, 1.047e-01, 8.848e-02, 7.851e-02, 6.619e-02, 5.837e-02, 5.167e-02, 4.713e-02, 4.163e-02, 3.675e-02, 3.496e-02, 3.439e-02, 3.440e-02, 3.523e-02, 3.650e-02, 3.978e-02, 4.264e-02]
    [5.356e+03, 2.092e+03, 1.044e+03, 5.072e+02, 1.812e+03, 1.699e+03, 1.602e+03, 2.223e+03, 1.862e+03, 1.800e+03, 2.059e+03, 1.036e+03, 5.836e+02, 3.619e+02, 1.683e+02, 9.231e+01, 3.076e+01, 1.410e+01, 1.229e+01, 7.481e+01, 2.993e+01, 1.381e+01, 7.521e+00, 4.571e+00, 2.099e+00, 1.169e+00, 4.449e-01, 2.534e-01, 1.418e-01, 1.066e-01, 8.968e-02, 7.935e-02, 6.674e-02, 5.876e-02, 5.197e-02, 4.740e-02, 4.189e-02, 3.705e-02, 3.532e-02, 3.482e-02, 3.487e-02, 3.578e-02, 3.712e-02, 4.055e-02, 4.353e-02]
    [5.718e+03, 2.240e+03, 1.120e+03, 4.704e+02, 1.644e+03, 1.542e+03, 1.452e+03, 2.317e+03, 1.963e+03, 1.638e+03, 1.874e+03, 1.095e+03, 6.165e+02, 3.832e+02, 1.785e+02, 9.800e+01, 3.270e+01, 1.499e+01, 1.143e+01, 6.876e+01, 3.139e+01, 1.452e+01, 7.926e+00, 4.822e+00, 2.215e+00, 1.232e+00, 4.647e-01, 2.618e-01, 1.440e-01, 1.074e-01, 8.992e-02, 7.933e-02, 6.647e-02, 5.846e-02, 5.166e-02, 4.710e-02, 4.164e-02, 3.692e-02, 3.527e-02, 3.482e-02, 3.491e-02, 3.591e-02, 3.730e-02, 4.084e-02, 4.387e-02]
    [6.169e+03, 2.426e+03, 1.214e+03, 4.441e+02, 4.427e+02, 1.513e+03, 1.422e+03, 1.337e+03, 1.847e+03, 1.671e+03, 1.512e+03, 1.731e+03, 1.170e+03, 6.589e+02, 4.101e+02, 1.915e+02, 1.053e+02, 3.518e+01, 1.613e+01, 1.079e+01, 6.414e+01, 3.330e+01, 1.544e+01, 8.448e+00, 5.147e+00, 2.365e+00, 1.314e+00, 4.916e-01, 2.742e-01, 1.485e-01, 1.097e-01, 9.134e-02, 8.035e-02, 6.711e-02, 5.894e-02, 5.204e-02, 4.744e-02, 4.197e-02, 3.728e-02, 3.568e-02, 3.529e-02, 3.542e-02, 3.650e-02, 3.797e-02, 4.166e-02, 4.481e-02]
    [6.538e+03, 2.579e+03, 1.292e+03, 4.730e+02, 4.106e+02, 1.355e+03, 1.287e+03, 1.215e+03, 1.664e+03, 1.518e+03, 1.379e+03, 1.582e+03, 1.227e+03, 6.912e+02, 4.308e+02, 2.017e+02, 1.110e+02, 3.715e+01, 1.704e+01, 1.003e+01, 5.898e+01, 3.465e+01, 1.614e+01, 8.850e+00, 5.399e+00, 2.481e+00, 1.377e+00, 5.115e-01, 2.827e-01, 1.506e-01, 1.103e-01, 9.134e-02, 8.010e-02, 6.669e-02, 5.849e-02, 5.159e-02, 4.702e-02, 4.162e-02, 3.704e-02, 3.552e-02, 3.518e-02, 3.537e-02, 3.651e-02, 3.802e-02, 4.181e-02, 4.501e-02]
    [7.039e+03, 2.790e+03, 1.401e+03, 5.136e+02, 3.887e+02, 1.274e+03, 1.200e+03, 1.126e+03, 1.547e+03, 1.409e+03, 1.282e+03, 1.468e+03, 1.305e+03, 7.385e+02, 4.610e+02, 2.164e+02, 1.193e+02, 3.998e+01, 1.836e+01, 9.527e+00, 5.539e+01, 3.668e+01, 1.720e+01, 9.444e+00, 5.766e+00, 2.651e+00, 1.470e+00, 5.426e-01, 2.972e-01, 1.560e-01, 1.131e-01, 9.321e-02, 8.153e-02, 6.766e-02, 5.921e-02, 5.217e-02, 4.754e-02, 4.209e-02, 3.754e-02, 3.606e-02, 3.577e-02, 3.601e-02, 3.723e-02, 3.882e-02, 4.276e-02, 4.609e-02]
    [7.350e+03, 2.931e+03, 1.473e+03, 5.414e+02, 3.575e+02, 1.152e+03, 1.083e+03, 1.013e+03, 1.389e+03, 1.170e+03, 1.157e+03, 1.324e+03, 7.685e+02, 4.793e+02, 2.254e+02, 1.244e+02, 4.178e+01, 1.920e+01, 8.809e+00, 5.065e+01, 3.765e+01, 1.778e+01, 9.779e+00, 5.975e+00, 2.751e+00, 1.524e+00, 5.593e-01, 3.038e-01, 1.571e-01, 1.129e-01, 9.250e-02, 8.064e-02, 6.670e-02, 5.826e-02, 5.129e-02, 4.673e-02, 4.139e-02, 3.698e-02, 3.559e-02, 3.536e-02, 3.563e-02, 3.691e-02, 3.853e-02, 4.253e-02, 4.587e-02]
    [7.809e+03, 3.131e+03, 1.578e+03, 5.808e+02, 3.356e+02, 1.046e+03, 9.930e+02, 9.313e+02, 1.261e+03, 1.231e+03, 1.066e+03, 1.223e+03, 8.134e+02, 5.072e+02, 2.391e+02, 1.321e+02, 4.445e+01, 2.044e+01, 8.316e+00, 4.733e+01, 3.949e+01, 1.873e+01, 1.030e+01, 6.306e+00, 2.907e+00, 1.609e+00, 5.876e-01, 3.167e-01, 1.614e-01, 1.149e-01, 9.371e-02, 8.138e-02, 6.707e-02, 5.849e-02, 5.144e-02, 4.684e-02, 4.151e-02, 3.715e-02, 3.582e-02, 3.564e-02, 3.596e-02, 3.730e-02, 3.898e-02, 4.311e-02, 4.654e-02]
    [8.157e+03, 3.296e+03, 1.665e+03, 6.143e+02, 3.114e+02, 9.285e+02, 9.393e+02, 8.469e+02, 1.145e+03, 1.060e+03, 9.712e+02, 1.117e+03, 8.471e+02, 5.294e+02, 2.500e+02, 1.384e+02, 4.664e+01, 2.146e+01, 7.760e+00, 4.360e+01, 4.121e+01, 1.942e+01, 1.070e+01, 6.564e+00, 3.029e+00, 1.676e+00, 6.091e-01, 3.260e-01, 1.639e-01, 1.156e-01, 9.374e-02, 8.113e-02, 6.662e-02, 5.800e-02, 5.095e-02, 4.638e-02, 4.112e-02, 3.686e-02, 3.561e-02, 3.548e-02, 3.583e-02, 3.724e-02, 3.895e-02, 4.315e-02, 4.662e-02]
    [8.582e+03, 3.491e+03, 1.767e+03, 6.536e+02, 3.169e+02, 2.918e+02, 8.691e+02, 8.308e+02, 7.776e+02, 1.050e+03, 9.743e+02, 8.939e+02, 1.029e+03, 8.846e+02, 5.569e+02, 2.631e+02, 1.459e+02, 4.923e+01, 2.268e+01, 7.631e+00, 7.307e+00, 4.073e+01, 2.027e+01, 1.120e+01, 6.879e+00, 3.176e+00, 1.758e+00, 6.361e-01, 3.381e-01, 1.677e-01, 1.172e-01, 9.453e-02, 8.153e-02, 6.670e-02, 5.797e-02, 5.086e-02, 4.628e-02, 4.105e-02, 3.686e-02, 3.567e-02, 3.559e-02, 3.598e-02, 3.745e-02, 3.921e-02, 4.351e-02, 4.704e-02]
    [8.434e+03, 8.380e+03, 8.326e+03, 8.684e+03, 3.608e+03, 1.832e+03, 6.792e+02, 3.297e+02, 2.678e+02, 7.882e+02, 7.504e+02, 6.995e+02, 9.445e+02, 8.782e+02, 8.062e+02, 9.292e+02, 9.014e+02, 5.721e+02, 2.702e+02, 1.501e+02, 5.078e+01, 2.341e+01, 7.878e+00, 6.738e+00, 3.719e+01, 2.064e+01, 1.145e+01, 7.041e+00, 3.255e+00, 1.801e+00, 6.492e-01, 3.429e-01, 1.679e-01, 1.163e-01, 9.328e-02, 8.022e-02, 6.538e-02, 5.669e-02, 4.967e-02, 4.518e-02, 4.009e-02, 3.606e-02, 3.494e-02, 3.492e-02, 3.534e-02, 3.683e-02, 3.860e-02, 4.290e-02, 4.642e-02]
    [9.096e+03, 8.465e+03, 7.863e+03, 8.198e+03, 3.919e+03, 1.997e+03, 7.420e+02, 3.607e+02, 2.592e+02, 7.550e+02, 7.123e+02, 6.636e+02, 8.943e+02, 8.430e+02, 7.665e+02, 8.837e+02, 6.173e+02, 2.922e+02, 1.626e+02, 5.512e+01, 2.543e+01, 8.561e+00, 6.553e+00, 3.582e+01, 2.210e+01, 1.232e+01, 7.579e+00, 3.510e+00, 1.942e+00, 6.978e-01, 3.663e-01, 1.771e-01, 1.217e-01, 9.701e-02, 8.313e-02, 6.749e-02, 5.841e-02, 5.111e-02, 4.647e-02, 4.124e-02, 3.716e-02, 3.607e-02, 3.608e-02, 3.655e-02, 3.815e-02, 4.002e-02, 4.455e-02, 4.823e-02]
    [9.413e+03, 8.151e+03, 7.035e+03, 7.338e+03, 4.085e+03, 2.088e+03, 7.780e+02, 3.787e+02, 2.408e+02, 6.941e+02, 6.392e+02, 6.044e+02, 8.181e+02, 7.579e+02, 6.991e+02, 8.064e+02, 6.376e+02, 3.032e+02, 1.690e+02, 5.743e+01, 2.652e+01, 8.930e+00, 6.129e+00, 3.316e+01, 2.270e+01, 1.272e+01, 7.825e+00, 3.633e+00, 2.011e+00, 7.202e-01, 3.760e-01, 1.797e-01, 1.223e-01, 9.699e-02, 8.281e-02, 6.696e-02, 5.785e-02, 5.054e-02, 4.594e-02, 4.078e-02, 3.681e-02, 3.577e-02, 3.583e-02, 3.634e-02, 3.797e-02, 3.987e-02, 4.445e-02, 4.815e-02]
    [9.365e+03, 8.775e+03, 8.214e+03, 8.685e+03, 7.576e+03, 6.584e+03, 6.888e+03, 4.335e+03, 2.226e+03, 8.319e+02, 4.055e+02, 2.303e+02, 2.290e+02, 6.674e+02, 6.184e+02, 5.645e+02, 7.692e+02, 7.146e+02, 6.556e+02, 7.547e+02, 6.711e+02, 3.214e+02, 1.793e+02, 6.104e+01, 2.822e+01, 9.507e+00, 5.863e+00, 3.143e+01, 2.381e+01, 1.340e+01, 8.248e+00, 3.836e+00, 2.124e+00, 7.589e-01, 3.941e-01, 1.863e-01, 1.257e-01, 9.912e-02, 8.431e-02, 6.789e-02, 5.854e-02, 5.108e-02, 4.641e-02, 4.121e-02, 3.725e-02, 3.625e-02, 3.635e-02, 3.689e-02, 3.860e-02, 4.057e-02, 4.529e-02, 4.910e-02]
    [8.543e+03, 7.990e+03, 7.465e+03, 8.547e+03, 7.957e+03, 7.404e+03, 7.837e+03, 6.861e+03, 5.985e+03, 6.255e+03, 4.499e+03, 2.319e+03, 8.696e+02, 4.246e+02, 2.414e+02, 2.135e+02, 6.098e+02, 5.634e+02, 5.169e+02, 7.016e+02, 6.507e+02, 6.013e+02, 6.930e+02, 6.898e+02, 3.334e+02, 1.860e+02, 6.347e+01, 2.938e+01, 9.904e+00, 5.498e+00, 2.919e+01, 2.457e+01, 1.379e+01, 8.511e+00, 3.963e+00, 2.196e+00, 7.828e-01, 4.046e-01, 1.891e-01, 1.265e-01, 9.923e-02, 8.410e-02, 6.744e-02, 5.803e-02, 5.058e-02, 4.592e-02, 4.078e-02, 3.692e-02, 3.598e-02, 3.612e-02, 3.669e-02, 3.844e-02, 4.042e-02, 4.518e-02, 4.902e-02]
    [9.087e+03, 7.988e+03, 7.000e+03, 8.025e+03, 7.447e+03, 6.911e+03, 7.321e+03, 6.440e+03, 5.652e+03, 5.905e+03, 4.772e+03, 2.464e+03, 9.267e+02, 4.531e+02, 2.578e+02, 2.039e+02, 5.764e+02, 5.302e+02, 4.846e+02, 6.545e+02, 6.319e+02, 5.654e+02, 6.518e+02, 3.529e+02, 1.967e+02, 6.731e+01, 3.119e+01, 1.052e+01, 5.271e+00, 2.772e+01, 2.579e+01, 1.447e+01, 8.962e+00, 4.177e+00, 2.315e+00, 8.239e-01, 4.239e-01, 1.961e-01, 1.301e-01, 1.015e-01, 8.570e-02, 6.843e-02, 5.876e-02, 5.110e-02, 4.640e-02, 4.122e-02, 3.737e-02, 3.646e-02, 3.664e-02, 3.726e-02, 3.907e-02, 4.113e-02, 4.603e-02, 4.996e-02]
    [9.711e+03, 7.991e+03, 6.563e+03, 7.545e+03, 6.984e+03, 6.465e+03, 6.853e+03, 6.031e+03, 5.293e+03, 5.532e+03, 5.033e+03, 2.607e+03, 9.857e+02, 4.811e+02, 2.740e+02, 1.943e+02, 5.454e+02, 4.908e+02, 4.554e+02, 6.188e+02, 5.756e+02, 5.332e+02, 6.149e+02, 3.732e+02, 2.082e+02, 7.143e+01, 3.312e+01, 1.119e+01, 5.215e+00, 5.066e+00, 2.635e+01, 1.520e+01, 9.447e+00, 4.409e+00, 2.445e+00, 8.687e-01, 4.452e-01, 2.039e-01, 1.342e-01, 1.041e-01, 8.757e-02, 6.962e-02, 5.961e-02, 5.181e-02, 4.701e-02, 4.177e-02, 3.792e-02, 3.705e-02, 3.727e-02, 3.792e-02, 3.981e-02, 4.194e-02, 4.699e-02, 5.103e-02]
    [1.058e+04, 8.122e+03, 6.278e+03, 7.224e+03, 6.661e+03, 6.142e+03, 6.513e+03, 5.090e+03, 5.006e+03, 5.235e+03, 2.768e+03, 1.047e+03, 5.131e+02, 2.924e+02, 1.868e+02, 5.214e+02, 5.145e+02, 4.310e+02, 5.857e+02, 5.455e+02, 5.060e+02, 5.836e+02, 3.950e+02, 2.209e+02, 7.597e+01, 3.526e+01, 1.192e+01, 5.557e+00, 4.892e+00, 2.518e+01, 1.599e+01, 9.977e+00, 4.664e+00, 2.588e+00, 9.180e-01, 4.687e-01, 2.126e-01, 1.389e-01, 1.071e-01, 8.976e-02, 7.105e-02, 6.070e-02, 5.268e-02, 4.779e-02, 4.244e-02, 3.858e-02, 3.774e-02, 3.800e-02, 3.870e-02, 4.067e-02, 4.288e-02, 4.809e-02, 5.226e-02]
    [6.627e+03, 6.806e+03, 6.949e+03, 8.554e+03, 7.579e+03, 5.933e+03, 6.833e+03, 6.264e+03, 5.744e+03, 6.093e+03, 5.273e+03, 4.738e+03, 4.951e+03, 2.878e+03, 1.093e+03, 5.366e+02, 3.061e+02, 1.927e+02, 1.767e+02, 4.892e+02, 4.487e+02, 4.013e+02, 5.456e+02, 5.135e+02, 4.723e+02, 5.448e+02, 4.094e+02, 2.300e+02, 7.925e+01, 3.684e+01, 1.247e+01, 5.809e+00, 4.642e+00, 2.366e+01, 1.650e+01, 1.033e+01, 4.839e+00, 2.687e+00, 9.522e-01, 4.844e-01, 2.178e-01, 1.412e-01, 1.083e-01, 9.040e-02, 7.127e-02, 6.072e-02, 5.262e-02, 4.769e-02, 4.236e-02, 3.856e-02, 3.776e-02, 3.806e-02, 3.879e-02, 4.081e-02, 4.304e-02, 4.832e-02, 5.257e-02]
    [2.056e+03, 2.007e+03, 1.959e+03, 2.729e+03, 3.894e+03, 5.830e+03, 7.242e+03, 7.232e+03, 5.687e+03, 6.555e+03, 5.985e+03, 5.466e+03, 5.799e+03, 5.553e+03, 4.497e+03, 4.699e+03, 3.048e+03, 1.162e+03, 5.709e+02, 3.260e+02, 2.053e+02, 1.702e+02, 4.678e+02, 4.226e+02, 3.805e+02, 5.174e+02, 4.884e+02, 4.494e+02, 5.184e+02, 4.314e+02, 2.440e+02, 8.411e+01, 3.916e+01, 1.327e+01, 6.181e+00, 4.491e+00, 2.265e+01, 1.735e+01, 1.087e+01, 5.107e+00, 2.840e+00, 1.005e+00, 5.098e-01, 2.273e-01, 1.462e-01, 1.115e-01, 9.276e-02, 7.280e-02, 6.188e-02, 5.350e-02, 4.849e-02, 4.308e-02, 3.925e-02, 3.849e-02, 3.882e-02, 3.959e-02, 4.169e-02, 4.401e-02, 4.946e-02, 5.380e-02]
    [2.107e+03, 1.963e+03, 1.827e+03, 2.635e+03, 3.837e+03, 5.613e+03, 6.852e+03, 6.641e+03, 5.262e+03, 6.072e+03, 5.358e+03, 5.046e+03, 5.355e+03, 4.740e+03, 4.189e+03, 4.376e+03, 3.120e+03, 1.193e+03, 5.873e+02, 3.356e+02, 2.115e+02, 1.587e+02, 4.334e+02, 3.898e+02, 3.496e+02, 4.756e+02, 4.501e+02, 4.141e+02, 4.777e+02, 4.401e+02, 2.499e+02, 8.633e+01, 4.025e+01, 1.365e+01, 6.362e+00, 4.208e+00, 2.100e+01, 1.774e+01, 1.107e+01, 5.212e+00, 2.901e+00, 1.027e+00, 5.192e-01, 2.296e-01, 1.466e-01, 1.112e-01, 9.218e-02, 7.201e-02, 6.106e-02, 5.271e-02, 4.773e-02, 4.240e-02, 3.868e-02, 3.797e-02, 3.833e-02, 3.912e-02, 4.124e-02, 4.355e-02, 4.899e-02, 5.335e-02]
    [2.216e+03, 1.978e+03, 1.763e+03, 2.443e+03, 3.617e+03, 5.416e+03, 6.540e+03, 6.291e+03, 5.031e+03, 5.810e+03, 5.624e+03, 4.771e+03, 5.064e+03, 4.492e+03, 3.980e+03, 4.158e+03, 3.278e+03, 1.256e+03, 6.193e+02, 3.542e+02, 2.234e+02, 1.522e+02, 4.127e+02, 3.696e+02, 3.302e+02, 4.492e+02, 3.989e+02, 3.921e+02, 4.524e+02, 2.629e+02, 9.087e+01, 4.242e+01, 1.441e+01, 6.716e+00, 4.051e+00, 2.001e+01, 1.850e+01, 1.155e+01, 5.455e+00, 3.040e+00, 1.076e+00, 5.425e-01, 2.380e-01, 1.509e-01, 1.139e-01, 9.404e-02, 7.312e-02, 6.186e-02, 5.331e-02, 4.822e-02, 4.285e-02, 3.913e-02, 3.845e-02, 3.885e-02, 3.967e-02, 4.185e-02, 4.422e-02, 4.980e-02, 5.423e-02]
    [2.291e+03, 1.960e+03, 1.668e+03, 1.931e+03, 2.527e+03, 3.961e+03, 4.764e+03, 5.041e+03, 4.701e+03, 5.432e+03, 4.900e+03, 4.421e+03, 4.694e+03, 4.164e+03, 3.691e+03, 3.854e+03, 3.360e+03, 1.292e+03, 6.380e+02, 3.653e+02, 2.305e+02, 1.429e+02, 3.844e+02, 3.427e+02, 3.049e+02, 4.149e+02, 4.068e+02, 3.631e+02, 4.190e+02, 2.693e+02, 9.335e+01, 4.363e+01, 1.484e+01, 6.920e+00, 3.859e+00, 3.812e+00, 1.864e+01, 1.175e+01, 5.573e+00, 3.109e+00, 1.100e+00, 5.534e-01, 2.410e-01, 1.517e-01, 1.139e-01, 9.371e-02, 7.252e-02, 6.120e-02, 5.262e-02, 4.759e-02, 4.228e-02, 3.865e-02, 3.802e-02, 3.844e-02, 3.928e-02, 4.147e-02, 4.384e-02, 4.943e-02, 5.385e-02]
    [2.396e+03, 1.956e+03, 1.591e+03, 2.337e+03, 3.515e+03, 5.023e+03, 5.928e+03, 5.314e+03, 4.464e+03, 5.164e+03, 4.635e+03, 4.166e+03, 4.424e+03, 3.929e+03, 3.482e+03, 3.638e+03, 3.507e+03, 1.354e+03, 6.697e+02, 3.838e+02, 2.423e+02, 1.368e+02, 3.658e+02, 3.133e+02, 2.881e+02, 3.925e+02, 3.684e+02, 3.441e+02, 3.970e+02, 2.815e+02, 9.802e+01, 4.588e+01, 1.563e+01, 7.288e+00, 4.064e+00, 3.672e+00, 1.777e+01, 1.223e+01, 5.826e+00, 3.253e+00, 1.151e+00, 5.775e-01, 2.498e-01, 1.562e-01, 1.167e-01, 9.562e-02, 7.365e-02, 6.196e-02, 5.321e-02, 4.808e-02, 4.272e-02, 3.908e-02, 3.848e-02, 3.894e-02, 3.981e-02, 4.206e-02, 4.449e-02, 5.017e-02, 5.470e-02]
    [2.494e+03, 1.953e+03, 1.521e+03, 2.173e+03, 3.293e+03, 4.745e+03, 5.551e+03, 5.550e+03, 4.229e+03, 4.896e+03, 4.382e+03, 3.924e+03, 4.168e+03, 3.467e+03, 3.286e+03, 3.433e+03, 1.405e+03, 6.953e+02, 3.988e+02, 2.520e+02, 1.299e+02, 3.437e+02, 3.269e+02, 2.695e+02, 3.672e+02, 3.452e+02, 3.228e+02, 3.725e+02, 2.902e+02, 1.016e+02, 4.765e+01, 1.625e+01, 7.582e+00, 4.227e+00, 3.500e+00, 1.676e+01, 1.259e+01, 6.012e+00, 3.360e+00, 1.189e+00, 5.953e-01, 2.558e-01, 1.590e-01, 1.181e-01, 9.644e-02, 7.393e-02, 6.204e-02, 5.318e-02, 4.801e-02, 4.265e-02, 3.905e-02, 3.848e-02, 3.896e-02, 3.986e-02, 4.214e-02, 4.460e-02, 5.033e-02, 5.492e-02]
    [2.616e+03, 1.961e+03, 1.462e+03, 2.108e+03, 3.193e+03, 4.528e+03, 5.239e+03, 5.847e+03, 4.038e+03, 4.677e+03, 4.161e+03, 3.703e+03, 3.934e+03, 3.590e+03, 3.127e+03, 3.266e+03, 1.465e+03, 7.264e+02, 4.170e+02, 2.636e+02, 1.271e+02, 1.242e+02, 3.283e+02, 2.889e+02, 2.540e+02, 3.463e+02, 3.259e+02, 3.051e+02, 3.520e+02, 3.012e+02, 1.060e+02, 4.980e+01, 1.701e+01, 7.940e+00, 4.425e+00, 3.361e+00, 1.592e+01, 1.309e+01, 6.244e+00, 3.492e+00, 1.236e+00, 6.178e-01, 2.639e-01, 1.629e-01, 1.205e-01, 9.800e-02, 7.477e-02, 6.257e-02, 5.351e-02, 4.828e-02, 4.289e-02, 3.930e-02, 3.877e-02, 3.927e-02, 4.020e-02, 4.253e-02, 4.504e-02, 5.088e-02, 5.551e-02]
    [2.748e+03, 1.978e+03, 1.408e+03, 2.069e+03, 3.170e+03, 4.339e+03, 4.952e+03, 6.069e+03, 3.841e+03, 4.452e+03, 3.523e+03, 3.499e+03, 3.717e+03, 3.337e+03, 2.995e+03, 3.127e+03, 1.526e+03, 7.587e+02, 4.359e+02, 2.757e+02, 1.330e+02, 1.190e+02, 3.126e+02, 2.799e+02, 2.397e+02, 3.271e+02, 3.080e+02, 2.886e+02, 3.330e+02, 3.129e+02, 1.106e+02, 5.204e+01, 1.780e+01, 8.315e+00, 4.634e+00, 3.232e+00, 1.514e+01, 1.362e+01, 6.478e+00, 3.628e+00, 1.285e+00, 6.415e-01, 2.724e-01, 1.672e-01, 1.230e-01, 9.968e-02, 7.569e-02, 6.317e-02, 5.392e-02, 4.860e-02, 4.317e-02, 3.958e-02, 3.907e-02, 3.961e-02, 4.056e-02, 4.294e-02, 4.549e-02, 5.141e-02, 5.613e-02]
    [2.899e+03, 1.995e+03, 1.362e+03, 1.919e+03, 3.937e+03, 4.145e+03, 4.830e+03, 4.446e+03, 3.668e+03, 4.254e+03, 3.686e+03, 3.326e+03, 3.534e+03, 3.160e+03, 2.821e+03, 2.945e+03, 1.594e+03, 7.946e+02, 4.569e+02, 2.892e+02, 1.397e+02, 1.146e+02, 2.991e+02, 2.609e+02, 2.274e+02, 3.101e+02, 2.830e+02, 2.745e+02, 3.167e+02, 1.157e+02, 5.453e+01, 1.868e+01, 8.735e+00, 4.867e+00, 3.122e+00, 1.200e+01, 1.409e+01, 6.741e+00, 3.780e+00, 1.340e+00, 6.682e-01, 2.822e-01, 1.722e-01, 1.261e-01, 1.018e-01, 7.693e-02, 6.404e-02, 5.455e-02, 4.912e-02, 4.362e-02, 4.002e-02, 3.954e-02, 4.010e-02, 4.108e-02, 4.352e-02, 4.612e-02, 5.216e-02, 5.698e-02]
    [3.017e+03, 1.350e+03, 1.300e+03, 1.965e+03, 2.949e+03, 3.908e+03, 4.540e+03, 4.200e+03, 3.495e+03, 4.054e+03, 3.797e+03, 3.128e+03, 3.323e+03, 2.970e+03, 2.652e+03, 2.769e+03, 1.640e+03, 8.193e+02, 4.717e+02, 2.988e+02, 1.444e+02, 1.088e+02, 2.824e+02, 2.511e+02, 2.128e+02, 2.906e+02, 2.893e+02, 2.577e+02, 2.973e+02, 1.193e+02, 5.628e+01, 1.932e+01, 9.040e+00, 5.038e+00, 3.147e+00, 2.975e+00, 1.365e+01, 6.909e+00, 3.881e+00, 1.378e+00, 6.860e-01, 2.882e-01, 1.749e-01, 1.274e-01, 1.025e-01, 7.710e-02, 6.397e-02, 5.439e-02, 4.895e-02, 4.347e-02, 3.989e-02, 3.944e-02, 4.002e-02, 4.101e-02, 4.347e-02, 4.609e-02, 5.218e-02, 5.700e-02]
    [3.187e+03, 1.424e+03, 1.264e+03, 1.597e+03, 2.302e+03, 3.442e+03, 3.935e+03, 3.452e+03, 3.352e+03, 3.890e+03, 3.397e+03, 2.969e+03, 3.155e+03, 2.826e+03, 2.531e+03, 2.640e+03, 1.710e+03, 8.560e+02, 4.934e+02, 3.129e+02, 1.513e+02, 1.049e+02, 2.703e+02, 2.211e+02, 2.019e+02, 2.757e+02, 2.676e+02, 2.450e+02, 2.826e+02, 1.247e+02, 5.881e+01, 2.023e+01, 9.472e+00, 5.279e+00, 3.297e+00, 2.874e+00, 1.305e+01, 7.161e+00, 4.033e+00, 1.433e+00, 7.130e-01, 2.981e-01, 1.799e-01, 1.305e-01, 1.046e-01, 7.829e-02, 6.478e-02, 5.496e-02, 4.941e-02, 4.385e-02, 4.028e-02, 3.985e-02, 4.045e-02, 4.147e-02, 4.398e-02, 4.664e-02, 5.282e-02, 5.773e-02]
    [3.335e+03, 1.489e+03, 1.203e+03, 1.505e+03, 2.189e+03, 3.273e+03, 3.682e+03, 3.598e+03, 3.152e+03, 3.659e+03, 3.182e+03, 2.769e+03, 2.943e+03, 2.637e+03, 2.363e+03, 2.465e+03, 1.768e+03, 8.859e+02, 5.113e+02, 3.244e+02, 1.571e+02, 9.997e+01, 2.557e+02, 2.301e+02, 1.894e+02, 2.589e+02, 2.522e+02, 2.306e+02, 2.659e+02, 1.290e+02, 6.087e+01, 2.098e+01, 9.828e+00, 5.478e+00, 3.420e+00, 2.751e+00, 1.237e+01, 7.352e+00, 4.154e+00, 1.477e+00, 7.339e-01, 3.054e-01, 1.834e-01, 1.324e-01, 1.058e-01, 7.880e-02, 6.502e-02, 5.505e-02, 4.944e-02, 4.387e-02, 4.030e-02, 3.989e-02, 4.052e-02, 4.155e-02, 4.409e-02, 4.677e-02, 5.301e-02, 5.796e-02]
    [3.510e+03, 1.566e+03, 1.154e+03, 1.417e+03, 2.053e+03, 3.082e+03, 3.421e+03, 3.771e+03, 2.985e+03, 3.464e+03, 3.003e+03, 2.604e+03, 2.768e+03, 2.486e+03, 2.233e+03, 2.329e+03, 1.838e+03, 9.222e+02, 5.328e+02, 3.382e+02, 1.639e+02, 9.599e+01, 2.443e+02, 2.379e+02, 1.791e+02, 2.449e+02, 2.393e+02, 2.182e+02, 2.518e+02, 1.340e+02, 6.334e+01, 2.187e+01, 1.025e+01, 5.717e+00, 3.569e+00, 2.652e+00, 1.180e+01, 7.587e+00, 4.302e+00, 1.531e+00, 7.598e-01, 3.149e-01, 1.881e-01, 1.352e-01, 1.076e-01, 7.981e-02, 6.567e-02, 5.545e-02, 4.977e-02, 4.413e-02, 4.057e-02, 4.018e-02, 4.082e-02, 4.188e-02, 4.446e-02, 4.717e-02, 5.350e-02, 5.852e-02]
    [3.683e+03, 1.643e+03, 1.108e+03, 1.327e+03, 1.911e+03, 2.901e+03, 3.170e+03, 3.922e+03, 2.828e+03, 3.279e+03, 2.833e+03, 2.445e+03, 2.599e+03, 2.339e+03, 2.104e+03, 2.194e+03, 1.902e+03, 9.564e+02, 5.534e+02, 3.514e+02, 1.705e+02, 9.691e+01, 9.201e+01, 2.334e+02, 1.983e+02, 1.689e+02, 2.312e+02, 2.268e+02, 2.065e+02, 2.382e+02, 1.389e+02, 6.573e+01, 2.273e+01, 1.067e+01, 5.949e+00, 3.713e+00, 2.552e+00, 1.123e+01, 7.810e+00, 4.438e+00, 1.581e+00, 7.844e-01, 3.238e-01, 1.925e-01, 1.378e-01, 1.093e-01, 8.066e-02, 6.618e-02, 5.577e-02, 5.000e-02, 4.433e-02, 4.075e-02, 4.038e-02, 4.103e-02, 4.210e-02, 4.472e-02, 4.747e-02, 5.384e-02, 5.893e-02]
    [3.872e+03, 1.729e+03, 1.147e+03, 1.152e+03, 1.251e+03, 2.689e+03, 3.802e+03, 3.773e+03, 2.696e+03, 3.124e+03, 2.686e+03, 2.309e+03, 2.454e+03, 2.210e+03, 1.992e+03, 2.078e+03, 1.972e+03, 9.943e+02, 5.759e+02, 3.660e+02, 1.778e+02, 1.011e+02, 8.858e+01, 2.234e+02, 1.964e+02, 1.600e+02, 2.191e+02, 2.079e+02, 1.961e+02, 2.262e+02, 1.440e+02, 6.835e+01, 2.367e+01, 1.112e+01, 6.206e+00, 3.872e+00, 2.464e+00, 1.073e+01, 8.069e+00, 4.587e+00, 1.637e+00, 8.119e-01, 3.339e-01, 1.976e-01, 1.409e-01, 1.114e-01, 8.179e-02, 6.688e-02, 5.627e-02, 5.038e-02, 4.463e-02, 4.105e-02, 4.068e-02, 4.137e-02, 4.246e-02, 4.511e-02, 4.790e-02, 5.437e-02, 5.953e-02]
    [4.032e+03, 1.801e+03, 1.023e+03, 2.003e+03, 2.218e+03, 2.622e+03, 2.864e+03, 2.852e+03, 2.546e+03, 2.948e+03, 2.524e+03, 2.161e+03, 2.296e+03, 1.938e+03, 1.869e+03, 1.949e+03, 1.023e+03, 5.936e+02, 3.776e+02, 1.836e+02, 1.045e+02, 8.458e+01, 2.121e+02, 1.860e+02, 1.503e+02, 2.060e+02, 1.956e+02, 1.846e+02, 2.129e+02, 1.478e+02, 7.039e+01, 2.443e+01, 1.149e+01, 6.414e+00, 4.002e+00, 2.360e+00, 1.016e+01, 8.290e+00, 4.696e+00, 1.680e+00, 8.327e-01, 3.414e-01, 2.011e-01, 1.428e-01, 1.125e-01, 8.224e-02, 6.705e-02, 5.625e-02, 5.034e-02, 4.458e-02, 4.100e-02, 4.065e-02, 4.134e-02, 4.244e-02, 4.511e-02, 4.791e-02, 5.442e-02, 5.956e-02]
    [4.243e+03, 1.898e+03, 1.032e+03, 9.882e+02, 1.066e+03, 1.492e+03, 2.478e+03, 2.608e+03, 2.621e+03, 2.424e+03, 2.800e+03, 2.393e+03, 2.041e+03, 2.166e+03, 2.011e+03, 1.767e+03, 1.843e+03, 1.063e+03, 6.178e+02, 3.935e+02, 1.914e+02, 1.090e+02, 8.155e+01, 2.038e+02, 1.702e+02, 1.426e+02, 1.959e+02, 1.933e+02, 1.756e+02, 2.025e+02, 1.530e+02, 7.317e+01, 2.546e+01, 1.199e+01, 6.693e+00, 4.176e+00, 2.284e+00, 9.728e+00, 8.585e+00, 4.855e+00, 1.740e+00, 8.628e-01, 3.525e-01, 2.068e-01, 1.463e-01, 1.149e-01, 8.357e-02, 6.794e-02, 5.688e-02, 5.083e-02, 4.501e-02, 4.139e-02, 4.104e-02, 4.174e-02, 4.286e-02, 4.558e-02, 4.844e-02, 5.502e-02, 6.024e-02]
    [4.433e+03, 1.986e+03, 1.081e+03, 9.506e+02, 1.034e+03, 1.431e+03, 2.341e+03, 2.487e+03, 2.512e+03, 2.307e+03, 2.663e+03, 1.965e+03, 1.923e+03, 2.041e+03, 1.844e+03, 1.671e+03, 1.742e+03, 1.100e+03, 6.402e+02, 4.083e+02, 1.987e+02, 1.132e+02, 7.844e+01, 1.946e+02, 1.618e+02, 1.349e+02, 1.853e+02, 1.848e+02, 1.666e+02, 1.921e+02, 1.578e+02, 7.574e+01, 2.641e+01, 1.245e+01, 6.954e+00, 4.339e+00, 2.203e+00, 9.301e+00, 8.731e+00, 4.993e+00, 1.795e+00, 8.896e-01, 3.625e-01, 2.118e-01, 1.492e-01, 1.168e-01, 8.456e-02, 6.857e-02, 5.727e-02, 5.112e-02, 4.522e-02, 4.160e-02, 4.124e-02, 4.196e-02, 4.310e-02, 4.584e-02, 4.872e-02, 5.537e-02, 6.064e-02]
    [4.652e+03, 2.089e+03, 1.137e+03, 9.187e+02, 9.971e+02, 1.386e+03, 2.258e+03, 2.389e+03, 2.380e+03, 2.203e+03, 2.541e+03, 2.049e+03, 1.822e+03, 1.933e+03, 1.748e+03, 1.585e+03, 1.652e+03, 1.144e+03, 6.661e+02, 4.253e+02, 2.072e+02, 1.181e+02, 7.582e+01, 1.870e+02, 1.546e+02, 1.283e+02, 1.764e+02, 1.766e+02, 1.588e+02, 1.830e+02, 1.637e+02, 7.883e+01, 2.752e+01, 1.298e+01, 7.256e+00, 4.528e+00, 2.185e+00, 2.137e+00, 8.904e+00, 5.158e+00, 1.860e+00, 9.214e-01, 3.744e-01, 2.180e-01, 1.530e-01, 1.194e-01, 8.603e-02, 6.953e-02, 5.794e-02, 5.167e-02, 4.570e-02, 4.201e-02, 4.166e-02, 4.239e-02, 4.355e-02, 4.633e-02, 4.926e-02, 5.598e-02, 6.136e-02]
    [4.830e+03, 2.174e+03, 1.184e+03, 8.773e+02, 9.925e+02, 1.407e+03, 2.151e+03, 2.316e+03, 2.257e+03, 2.080e+03, 2.400e+03, 2.117e+03, 1.704e+03, 1.808e+03, 1.638e+03, 1.486e+03, 1.549e+03, 1.179e+03, 6.869e+02, 4.387e+02, 2.140e+02, 1.221e+02, 7.266e+01, 1.780e+02, 1.464e+02, 1.209e+02, 1.663e+02, 1.674e+02, 1.501e+02, 1.728e+02, 1.681e+02, 8.123e+01, 2.841e+01, 1.342e+01, 7.504e+00, 4.683e+00, 2.259e+00, 2.055e+00, 8.464e+00, 5.279e+00, 1.909e+00, 9.456e-01, 3.834e-01, 2.224e-01, 1.555e-01, 1.210e-01, 8.679e-02, 6.993e-02, 5.814e-02, 5.179e-02, 4.575e-02, 4.207e-02, 4.172e-02, 4.246e-02, 4.362e-02, 4.643e-02, 4.937e-02, 5.613e-02, 6.154e-02]
    [5.008e+03, 2.259e+03, 1.231e+03, 8.352e+02, 1.136e+03, 1.582e+03, 2.049e+03, 2.364e+03, 2.207e+03, 1.958e+03, 2.267e+03, 2.188e+03, 1.591e+03, 1.687e+03, 1.530e+03, 1.392e+03, 1.452e+03, 1.212e+03, 7.068e+02, 4.518e+02, 2.208e+02, 1.260e+02, 6.957e+01, 1.693e+02, 1.473e+02, 1.139e+02, 1.572e+02, 1.497e+02, 1.416e+02, 1.632e+02, 8.361e+01, 2.929e+01, 1.385e+01, 7.751e+00, 4.838e+00, 2.332e+00, 1.976e+00, 8.046e+00, 5.398e+00, 1.957e+00, 9.696e-01, 3.923e-01, 2.267e-01, 1.580e-01, 1.226e-01, 8.751e-02, 7.031e-02, 5.832e-02, 5.187e-02, 4.581e-02, 4.210e-02, 4.175e-02, 4.248e-02, 4.366e-02, 4.647e-02, 4.943e-02, 5.622e-02, 6.162e-02]
    [5.210e+03, 2.356e+03, 1.285e+03, 8.006e+02, 1.397e+03, 1.726e+03, 1.944e+03, 2.458e+03, 1.965e+03, 1.857e+03, 2.146e+03, 1.796e+03, 1.496e+03, 1.585e+03, 1.442e+03, 1.311e+03, 1.368e+03, 1.251e+03, 7.304e+02, 4.672e+02, 2.287e+02, 1.306e+02, 6.701e+01, 1.621e+02, 1.116e+02, 1.078e+02, 1.485e+02, 1.416e+02, 1.344e+02, 1.548e+02, 8.636e+01, 3.032e+01, 1.436e+01, 8.041e+00, 5.021e+00, 2.419e+00, 1.910e+00, 7.683e+00, 5.549e+00, 2.014e+00, 9.985e-01, 4.031e-01, 2.323e-01, 1.614e-01, 1.248e-01, 8.870e-02, 7.102e-02, 5.876e-02, 5.222e-02, 4.606e-02, 4.234e-02, 4.197e-02, 4.272e-02, 4.391e-02, 4.675e-02, 4.972e-02, 5.658e-02, 6.206e-02]
    [5.441e+03, 2.468e+03, 1.348e+03, 7.724e+02, 1.777e+03, 1.850e+03, 1.852e+03, 2.576e+03, 2.053e+03, 1.774e+03, 2.048e+03, 1.707e+03, 1.415e+03, 1.498e+03, 1.366e+03, 1.243e+03, 1.297e+03, 1.296e+03, 7.580e+02, 4.855e+02, 2.378e+02, 1.360e+02, 6.491e+01, 1.560e+02, 1.160e+02, 1.027e+02, 1.416e+02, 1.351e+02, 1.282e+02, 1.478e+02, 8.952e+01, 3.152e+01, 1.495e+01, 8.379e+00, 5.233e+00, 2.522e+00, 1.856e+00, 7.380e+00, 5.739e+00, 2.082e+00, 1.033e+00, 4.163e-01, 2.391e-01, 1.656e-01, 1.277e-01, 9.036e-02, 7.214e-02, 5.955e-02, 5.285e-02, 4.659e-02, 4.279e-02, 4.242e-02, 4.317e-02, 4.437e-02, 4.725e-02, 5.025e-02, 5.721e-02, 6.276e-02]
    [5.724e+03, 2.604e+03, 1.423e+03, 7.482e+02, 2.206e+03, 1.941e+03, 1.775e+03, 2.711e+03, 2.155e+03, 1.693e+03, 1.956e+03, 1.622e+03, 1.339e+03, 1.419e+03, 1.299e+03, 1.190e+03, 1.242e+03, 7.931e+02, 5.085e+02, 2.494e+02, 1.427e+02, 6.337e+01, 1.513e+02, 1.219e+02, 9.849e+01, 1.361e+02, 1.297e+02, 1.232e+02, 1.420e+02, 9.352e+01, 3.303e+01, 1.569e+01, 8.802e+00, 5.499e+00, 2.649e+00, 1.820e+00, 7.140e+00, 5.991e+00, 2.170e+00, 1.078e+00, 4.335e-01, 2.483e-01, 1.714e-01, 1.318e-01, 9.286e-02, 7.391e-02, 6.087e-02, 5.394e-02, 4.749e-02, 4.362e-02, 4.323e-02, 4.399e-02, 4.522e-02, 4.816e-02, 5.124e-02, 5.835e-02, 6.398e-02]
    [5.868e+03, 5.651e+03, 5.435e+03, 5.551e+03, 2.731e+03, 1.495e+03, 7.225e+02, 2.431e+03, 1.928e+03, 1.686e+03, 2.763e+03, 2.250e+03, 1.614e+03, 1.866e+03, 1.275e+03, 1.269e+03, 1.345e+03, 1.234e+03, 1.126e+03, 1.175e+03, 8.251e+02, 5.299e+02, 2.601e+02, 1.490e+02, 6.162e+01, 1.461e+02, 1.279e+02, 9.417e+01, 1.302e+02, 1.338e+02, 1.181e+02, 1.360e+02, 9.704e+01, 3.442e+01, 1.638e+01, 9.196e+00, 5.748e+00, 2.769e+00, 1.777e+00, 6.895e+00, 6.174e+00, 2.249e+00, 1.118e+00, 4.491e-01, 2.565e-01, 1.765e-01, 1.354e-01, 9.495e-02, 7.538e-02, 6.189e-02, 5.479e-02, 4.821e-02, 4.424e-02, 4.383e-02, 4.461e-02, 4.585e-02, 4.883e-02, 5.195e-02, 5.918e-02, 6.493e-02]
    [5.826e+03, 5.354e+03, 4.909e+03, 5.013e+03, 2.719e+03, 1.490e+03, 6.634e+02, 2.319e+03, 1.554e+03, 1.524e+03, 2.470e+03, 1.867e+03, 1.479e+03, 1.710e+03, 1.266e+03, 1.148e+03, 1.217e+03, 1.112e+03, 1.017e+03, 1.061e+03, 8.163e+02, 5.240e+02, 2.577e+02, 1.477e+02, 5.697e+01, 1.344e+02, 1.259e+02, 8.557e+01, 1.185e+02, 1.225e+02, 1.077e+02, 1.241e+02, 9.563e+01, 3.408e+01, 1.624e+01, 9.125e+00, 5.706e+00, 2.749e+00, 1.649e+00, 6.371e+00, 6.086e+00, 2.215e+00, 1.101e+00, 4.420e-01, 2.518e-01, 1.728e-01, 1.322e-01, 9.230e-02, 7.303e-02, 5.984e-02, 5.290e-02, 4.649e-02, 4.264e-02, 4.224e-02, 4.298e-02, 4.418e-02, 4.705e-02, 5.007e-02, 5.704e-02, 6.260e-02]
    [6.238e+03, 5.356e+03, 4.673e+03, 4.772e+03, 2.846e+03, 1.562e+03, 6.414e+02, 1.995e+03, 1.994e+03, 1.449e+03, 2.255e+03, 1.761e+03, 1.415e+03, 1.641e+03, 1.322e+03, 1.086e+03, 1.153e+03, 1.059e+03, 9.666e+02, 1.008e+03, 8.489e+02, 5.451e+02, 2.684e+02, 1.539e+02, 5.573e+01, 5.544e+01, 1.304e+02, 1.031e+02, 8.184e+01, 1.137e+02, 1.179e+02, 1.031e+02, 1.187e+02, 9.933e+01, 3.550e+01, 1.694e+01, 9.525e+00, 5.959e+00, 2.871e+00, 1.655e+00, 1.610e+00, 6.089e+00, 2.295e+00, 1.141e+00, 4.577e-01, 2.601e-01, 1.780e-01, 1.358e-01, 9.444e-02, 7.450e-02, 6.087e-02, 5.376e-02, 4.721e-02, 4.324e-02, 4.283e-02, 4.358e-02, 4.479e-02, 4.769e-02, 5.077e-02, 5.786e-02, 6.350e-02]
    [6.201e+03, 5.895e+03, 5.602e+03, 5.683e+03, 5.019e+03, 4.424e+03, 4.516e+03, 2.950e+03, 1.620e+03, 6.664e+02, 6.169e+02, 1.715e+03, 1.506e+03, 1.374e+03, 2.039e+03, 1.647e+03, 1.342e+03, 1.558e+03, 1.367e+03, 1.024e+03, 1.086e+03, 9.995e+02, 9.129e+02, 9.522e+02, 8.741e+02, 5.613e+02, 2.769e+02, 1.589e+02, 5.760e+01, 5.355e+01, 1.253e+02, 9.839e+01, 7.766e+01, 1.081e+02, 1.126e+02, 9.799e+01, 1.128e+02, 1.023e+02, 3.664e+01, 1.750e+01, 9.850e+00, 6.166e+00, 2.971e+00, 1.712e+00, 1.560e+00, 5.826e+00, 2.355e+00, 1.172e+00, 4.696e-01, 2.662e-01, 1.817e-01, 1.383e-01, 9.579e-02, 7.535e-02, 6.141e-02, 5.415e-02, 4.751e-02, 4.348e-02, 4.304e-02, 4.379e-02, 4.500e-02, 4.793e-02, 5.102e-02, 5.815e-02, 6.383e-02]
    [6.469e+03, 6.034e+03, 5.622e+03, 5.702e+03, 4.905e+03, 4.203e+03, 4.289e+03, 3.082e+03, 1.696e+03, 6.981e+02, 5.959e+02, 1.537e+03, 1.404e+03, 1.307e+03, 1.892e+03, 1.564e+03, 1.296e+03, 1.504e+03, 1.426e+03, 9.745e+02, 1.034e+03, 8.687e+02, 8.678e+02, 9.051e+02, 5.829e+02, 2.878e+02, 1.653e+02, 6.002e+01, 5.213e+01, 1.214e+02, 1.042e+02, 7.426e+01, 1.036e+02, 1.079e+02, 9.403e+01, 1.082e+02, 1.062e+02, 3.811e+01, 1.823e+01, 1.027e+01, 6.433e+00, 3.100e+00, 1.786e+00, 1.525e+00, 5.622e+00, 2.434e+00, 1.213e+00, 4.859e-01, 2.749e-01, 1.872e-01, 1.421e-01, 9.804e-02, 7.686e-02, 6.251e-02, 5.504e-02, 4.822e-02, 4.409e-02, 4.363e-02, 4.438e-02, 4.560e-02, 4.856e-02, 5.171e-02, 5.895e-02, 6.473e-02]
    [6.614e+03, 5.747e+03, 4.976e+03, 5.048e+03, 4.463e+03, 3.937e+03, 4.017e+03, 3.161e+03, 1.742e+03, 7.180e+02, 5.671e+02, 1.394e+03, 1.304e+03, 1.226e+03, 1.749e+03, 1.253e+03, 1.217e+03, 1.415e+03, 1.137e+03, 9.103e+02, 9.655e+02, 8.878e+02, 8.129e+02, 8.477e+02, 5.945e+02, 2.939e+02, 1.689e+02, 6.141e+01, 4.991e+01, 1.156e+02, 9.924e+01, 6.984e+01, 9.527e+01, 9.368e+01, 8.851e+01, 1.018e+02, 3.892e+01, 1.865e+01, 1.052e+01, 6.592e+00, 3.178e+00, 1.830e+00, 1.465e+00, 5.336e+00, 2.472e+00, 1.234e+00, 4.939e-01, 2.789e-01, 1.895e-01, 1.435e-01, 9.861e-02, 7.709e-02, 6.251e-02, 5.498e-02, 4.812e-02, 4.396e-02, 4.347e-02, 4.421e-02, 4.542e-02, 4.836e-02, 5.149e-02, 5.871e-02, 6.447e-02]
    [6.530e+03, 6.490e+03, 6.451e+03, 6.868e+03, 5.755e+03, 4.794e+03, 4.863e+03, 4.311e+03, 3.815e+03, 3.891e+03, 3.327e+03, 1.834e+03, 7.558e+02, 5.548e+02, 1.363e+03, 1.266e+03, 1.185e+03, 1.695e+03, 1.315e+03, 1.182e+03, 1.374e+03, 8.759e+02, 8.755e+02, 9.288e+02, 8.514e+02, 7.810e+02, 8.144e+02, 6.217e+02, 3.074e+02, 1.769e+02, 6.442e+01, 4.903e+01, 1.130e+02, 7.025e+01, 6.747e+01, 9.452e+01, 8.995e+01, 8.576e+01, 9.861e+01, 4.077e+01, 1.957e+01, 1.105e+01, 6.929e+00, 3.342e+00, 1.924e+00, 1.445e+00, 5.198e+00, 2.575e+00, 1.288e+00, 5.152e-01, 2.904e-01, 1.969e-01, 1.487e-01, 1.018e-01, 7.937e-02, 6.420e-02, 5.637e-02, 4.927e-02, 4.496e-02, 4.445e-02, 4.519e-02, 4.641e-02, 4.943e-02, 5.261e-02, 6.000e-02, 6.592e-02]
    [6.626e+03, 6.375e+03, 6.127e+03, 6.519e+03, 5.446e+03, 4.526e+03, 4.589e+03, 4.065e+03, 3.598e+03, 3.668e+03, 3.382e+03, 1.865e+03, 7.692e+02, 5.257e+02, 1.266e+03, 1.188e+03, 1.112e+03, 1.582e+03, 1.329e+03, 1.110e+03, 1.292e+03, 8.891e+02, 8.118e+02, 8.611e+02, 7.915e+02, 7.282e+02, 7.592e+02, 6.284e+02, 3.108e+02, 1.791e+02, 6.528e+01, 4.663e+01, 1.070e+02, 7.106e+01, 6.300e+01, 8.838e+01, 9.515e+01, 8.023e+01, 9.222e+01, 4.128e+01, 1.983e+01, 1.121e+01, 7.035e+00, 3.395e+00, 1.954e+00, 1.378e+00, 4.893e+00, 2.591e+00, 1.298e+00, 5.192e-01, 2.922e-01, 1.976e-01, 1.490e-01, 1.016e-01, 7.896e-02, 6.370e-02, 5.587e-02, 4.878e-02, 4.447e-02, 4.392e-02, 4.463e-02, 4.583e-02, 4.879e-02, 5.195e-02, 5.927e-02, 6.512e-02]
    };

    E_cell = {
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.03542e-03, 1.07210e-03, 1.07210e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.14237e-03, 1.30500e-03, 1.30500e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.55960e-03, 1.55960e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.83890e-03, 1.83890e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.14550e-03, 2.14550e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.47200e-03, 2.47200e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.82240e-03, 2.82240e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.20290e-03, 3.20290e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.60740e-03, 3.60740e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 4.03810e-03, 4.03810e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 4.49280e-03, 4.49280e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 4.96640e-03, 4.96640e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 5.46510e-03, 5.46510e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 5.98920e-03, 5.98920e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 6.53900e-03, 6.53900e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 7.11200e-03, 7.11200e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 7.70890e-03, 7.70890e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.00404e-03, 1.00810e-03, 1.00810e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 8.33280e-03, 8.33280e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.04695e-03, 1.09610e-03, 1.09610e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 8.97890e-03, 8.97890e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.00980e-03, 1.01970e-03, 1.01970e-03, 1.03119e-03, 1.04280e-03, 1.04280e-03, 1.11565e-03, 1.19360e-03, 1.19360e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 9.65860e-03, 9.65860e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.05613e-03, 1.11540e-03, 1.11540e-03, 1.12877e-03, 1.14230e-03, 1.14230e-03, 1.21752e-03, 1.29770e-03, 1.29770e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.03671e-02, 1.03671e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.10304e-03, 1.21670e-03, 1.21670e-03, 1.23215e-03, 1.24780e-03, 1.24780e-03, 1.32844e-03, 1.41430e-03, 1.41430e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.11031e-02, 1.11031e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.15026e-03, 1.32310e-03, 1.32310e-03, 1.34073e-03, 1.35860e-03, 1.35860e-03, 1.50000e-03, 1.52650e-03, 1.52650e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.18667e-02, 1.18667e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.19825e-03, 1.43580e-03, 1.43580e-03, 1.45586e-03, 1.47620e-03, 1.47620e-03, 1.50000e-03, 1.65390e-03, 1.65390e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.26578e-02, 1.26578e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.54990e-03, 1.54990e-03, 1.57278e-03, 1.59600e-03, 1.59600e-03, 1.68644e-03, 1.78200e-03, 1.78200e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.34737e-02, 1.34737e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.67490e-03, 1.67490e-03, 1.70085e-03, 1.72720e-03, 1.72720e-03, 1.82152e-03, 1.92100e-03, 1.92100e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.43256e-02, 1.43256e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.80440e-03, 1.80440e-03, 1.83391e-03, 1.86390e-03, 1.86390e-03, 2.00000e-03, 2.06510e-03, 2.06510e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.51997e-02, 1.51997e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.93960e-03, 1.93960e-03, 2.00000e-03, 2.00680e-03, 2.00680e-03, 2.10895e-03, 2.21630e-03, 2.21630e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.61046e-02, 1.61046e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.08000e-03, 2.08000e-03, 2.11741e-03, 2.15550e-03, 2.15550e-03, 2.26140e-03, 2.37250e-03, 2.37250e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.70384e-02, 1.70384e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.22230e-03, 2.22230e-03, 2.26411e-03, 2.30670e-03, 2.30670e-03, 2.41654e-03, 2.53160e-03, 2.53160e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.79976e-02, 1.79976e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.37050e-03, 2.37050e-03, 2.41714e-03, 2.46470e-03, 2.46470e-03, 2.57857e-03, 2.69770e-03, 2.69770e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.89856e-02, 1.89856e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.52020e-03, 2.52020e-03, 2.57212e-03, 2.62510e-03, 2.62510e-03, 2.74267e-03, 2.86550e-03, 2.86550e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.99995e-02, 1.99995e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.67690e-03, 2.67690e-03, 2.73443e-03, 2.79320e-03, 2.79320e-03, 3.00000e-03, 3.04250e-03, 3.04250e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 2.10440e-02, 2.10440e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.83790e-03, 2.83790e-03, 2.90168e-03, 2.96690e-03, 2.96690e-03, 3.00000e-03, 3.22400e-03, 3.22400e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 2.21172e-02, 2.21172e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.00380e-03, 3.00380e-03, 3.07413e-03, 3.14610e-03, 3.14610e-03, 3.27631e-03, 3.41190e-03, 3.41190e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 2.32199e-02, 2.32199e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.17330e-03, 3.17330e-03, 3.25085e-03, 3.33030e-03, 3.33030e-03, 3.46459e-03, 3.60430e-03, 3.60430e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 2.43503e-02, 2.43503e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.35110e-03, 3.35110e-03, 3.43632e-03, 3.52370e-03, 3.52370e-03, 3.66203e-03, 3.80580e-03, 3.80580e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 2.55140e-02, 2.55140e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.53750e-03, 3.53750e-03, 3.63101e-03, 3.72700e-03, 3.72700e-03, 4.00000e-03, 4.01800e-03, 4.01800e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 2.67112e-02, 2.67112e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.73010e-03, 3.73010e-03, 3.83264e-03, 3.93800e-03, 3.93800e-03, 4.00000e-03, 4.23750e-03, 4.23750e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 2.79399e-02, 2.79399e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.92880e-03, 3.92880e-03, 4.00000e-03, 4.15610e-03, 4.15610e-03, 4.30764e-03, 4.46470e-03, 4.46470e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 2.92001e-02, 2.92001e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 4.13220e-03, 4.13220e-03, 4.25449e-03, 4.38040e-03, 4.38040e-03, 4.53657e-03, 4.69830e-03, 4.69830e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 3.04912e-02, 3.04912e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.00300e-03, 1.00600e-03, 1.00600e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 4.34140e-03, 4.34140e-03, 4.47465e-03, 4.61200e-03, 4.61200e-03, 4.77280e-03, 4.93920e-03, 4.93920e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 3.18138e-02, 3.18138e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.03542e-03, 1.07210e-03, 1.07210e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 4.55710e-03, 4.55710e-03, 4.70229e-03, 4.85210e-03, 4.85210e-03, 5.00000e-03, 5.18810e-03, 5.18810e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 3.31694e-02, 3.31694e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.07191e-03, 1.14900e-03, 1.14900e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 4.78220e-03, 4.78220e-03, 5.00000e-03, 5.10370e-03, 5.10370e-03, 5.27536e-03, 5.45280e-03, 5.45280e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 3.45614e-02, 3.45614e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.03199e-03, 1.06500e-03, 1.06500e-03, 1.13851e-03, 1.21710e-03, 1.21710e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 5.01190e-03, 5.01190e-03, 5.18274e-03, 5.35940e-03, 5.35940e-03, 5.53401e-03, 5.71430e-03, 5.71430e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 3.59846e-02, 3.59846e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.03063e-03, 1.06220e-03, 1.06220e-03, 1.09882e-03, 1.13670e-03, 1.13670e-03, 1.21224e-03, 1.29280e-03, 1.29280e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 5.24700e-03, 5.24700e-03, 5.43204e-03, 5.62360e-03, 5.62360e-03, 5.80333e-03, 5.98880e-03, 5.98880e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 3.74406e-02, 3.74406e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.05991e-03, 1.12340e-03, 1.12340e-03, 1.16320e-03, 1.20440e-03, 1.20440e-03, 1.28045e-03, 1.36130e-03, 1.36130e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 5.48270e-03, 5.48270e-03, 5.68299e-03, 5.89060e-03, 5.89060e-03, 6.00000e-03, 6.26630e-03, 6.26630e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 3.89246e-02, 3.89246e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.08876e-03, 1.18540e-03, 1.18540e-03, 1.22832e-03, 1.27280e-03, 1.27280e-03, 1.35222e-03, 1.43660e-03, 1.43660e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 5.72340e-03, 5.72340e-03, 6.00000e-03, 6.16420e-03, 6.16420e-03, 6.35359e-03, 6.54880e-03, 6.54880e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 4.04430e-02, 4.04430e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.11454e-03, 1.24220e-03, 1.24220e-03, 1.28892e-03, 1.33740e-03, 1.33740e-03, 1.50000e-03, 1.51100e-03, 1.51100e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 5.96430e-03, 5.96430e-03, 6.00000e-03, 6.44040e-03, 6.44040e-03, 6.63467e-03, 6.83480e-03, 6.83480e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 4.19906e-02, 4.19906e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.00250e-03, 1.00500e-03, 1.00500e-03, 1.14188e-03, 1.29740e-03, 1.29740e-03, 1.34907e-03, 1.40280e-03, 1.40280e-03, 1.50000e-03, 1.57530e-03, 1.57530e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 6.20790e-03, 6.20790e-03, 6.45960e-03, 6.72150e-03, 6.72150e-03, 6.92080e-03, 7.12600e-03, 7.12600e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 4.35689e-02, 4.35689e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.01336e-03, 1.02690e-03, 1.02690e-03, 1.03913e-03, 1.05150e-03, 1.05150e-03, 1.19448e-03, 1.35690e-03, 1.35690e-03, 1.41299e-03, 1.47140e-03, 1.47140e-03, 1.50000e-03, 1.65300e-03, 1.65300e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 6.45930e-03, 6.45930e-03, 6.73036e-03, 7.01280e-03, 7.01280e-03, 7.21737e-03, 7.42790e-03, 7.42790e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 4.51840e-02, 4.51840e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.03933e-03, 1.08020e-03, 1.08020e-03, 1.09302e-03, 1.10600e-03, 1.10600e-03, 1.25312e-03, 1.41980e-03, 1.41980e-03, 1.50000e-03, 1.54070e-03, 1.54070e-03, 1.62921e-03, 1.72280e-03, 1.72280e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 6.71620e-03, 6.71620e-03, 7.00767e-03, 7.31180e-03, 7.31180e-03, 7.52130e-03, 7.73680e-03, 7.73680e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 4.68342e-02, 4.68342e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.06344e-03, 1.13090e-03, 1.13090e-03, 1.14565e-03, 1.16060e-03, 1.16060e-03, 1.31087e-03, 1.48060e-03, 1.48060e-03, 1.50000e-03, 1.61390e-03, 1.61390e-03, 1.70441e-03, 1.80000e-03, 1.80000e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 6.97690e-03, 6.97690e-03, 7.28997e-03, 7.61710e-03, 7.61710e-03, 8.00000e-03, 8.05200e-03, 8.05200e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 4.85190e-02, 4.85190e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.08867e-03, 1.18520e-03, 1.18520e-03, 1.20109e-03, 1.21720e-03, 1.21720e-03, 1.50000e-03, 1.54400e-03, 1.54400e-03, 1.61454e-03, 1.68830e-03, 1.68830e-03, 1.78195e-03, 1.88080e-03, 1.88080e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 7.24280e-03, 7.24280e-03, 7.57876e-03, 7.93030e-03, 7.93030e-03, 8.00000e-03, 8.37560e-03, 8.37560e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 5.02391e-02, 5.02391e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.11409e-03, 1.24120e-03, 1.24120e-03, 1.25799e-03, 1.27500e-03, 1.27500e-03, 1.50000e-03, 1.61130e-03, 1.61130e-03, 1.68769e-03, 1.76770e-03, 1.76770e-03, 1.86493e-03, 1.96750e-03, 1.96750e-03, 2.00000e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 7.51400e-03, 7.51400e-03, 8.00000e-03, 8.25160e-03, 8.25160e-03, 8.47673e-03, 8.70800e-03, 8.70800e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 5.19957e-02, 5.19957e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.13794e-03, 1.29490e-03, 1.29490e-03, 1.31356e-03, 1.33250e-03, 1.33250e-03, 1.50000e-03, 1.67560e-03, 1.67560e-03, 1.75674e-03, 1.84180e-03, 1.84180e-03, 2.00000e-03, 2.04680e-03, 2.04680e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 7.79010e-03, 7.79010e-03, 8.00000e-03, 8.58060e-03, 8.58060e-03, 8.81013e-03, 9.04580e-03, 9.04580e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 5.37885e-02, 5.37885e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.16250e-03, 1.35140e-03, 1.35140e-03, 1.37130e-03, 1.39150e-03, 1.39150e-03, 1.50000e-03, 1.74120e-03, 1.74120e-03, 1.82975e-03, 1.92280e-03, 1.92280e-03, 2.00000e-03, 2.12830e-03, 2.12830e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 8.07110e-03, 8.07110e-03, 8.48389e-03, 8.91780e-03, 8.91780e-03, 9.15290e-03, 9.39420e-03, 9.39420e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 5.56177e-02, 5.56177e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.18714e-03, 1.40930e-03, 1.40930e-03, 1.43113e-03, 1.45330e-03, 1.45330e-03, 1.50000e-03, 1.81180e-03, 1.81180e-03, 2.00000e-03, 2.00580e-03, 2.00580e-03, 2.10376e-03, 2.20650e-03, 2.20650e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 8.35790e-03, 8.35790e-03, 8.79944e-03, 9.26430e-03, 9.26430e-03, 9.50468e-03, 9.75130e-03, 9.75130e-03, 1.00000e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 5.74855e-02, 5.74855e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.21149e-03, 1.46770e-03, 1.46770e-03, 1.50000e-03, 1.51460e-03, 1.51460e-03, 1.68946e-03, 1.88450e-03, 1.88450e-03, 2.00000e-03, 2.08980e-03, 2.08980e-03, 2.19562e-03, 2.30680e-03, 2.30680e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 8.64800e-03, 8.64800e-03, 9.11959e-03, 9.61690e-03, 9.61690e-03, 1.00000e-02, 1.01157e-02, 1.01157e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 5.93896e-02, 5.93896e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.52780e-03, 1.52780e-03, 1.55186e-03, 1.57630e-03, 1.57630e-03, 1.75313e-03, 1.94980e-03, 1.94980e-03, 2.00000e-03, 2.17300e-03, 2.17300e-03, 2.28278e-03, 2.39810e-03, 2.39810e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 8.94360e-03, 8.94360e-03, 9.44675e-03, 9.97820e-03, 9.97820e-03, 1.00000e-02, 1.04864e-02, 1.04864e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 6.13323e-02, 6.13323e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.58850e-03, 1.58850e-03, 1.61375e-03, 1.63940e-03, 1.63940e-03, 2.00000e-03, 2.02360e-03, 2.02360e-03, 2.14019e-03, 2.26350e-03, 2.26350e-03, 2.37462e-03, 2.49120e-03, 2.49120e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 9.24410e-03, 9.24410e-03, 1.00000e-02, 1.03486e-02, 1.03486e-02, 1.06063e-02, 1.08704e-02, 1.08704e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 6.33138e-02, 6.33138e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.66170e-03, 1.66170e-03, 1.68883e-03, 1.71640e-03, 1.71640e-03, 2.00000e-03, 2.10760e-03, 2.10760e-03, 2.23278e-03, 2.36540e-03, 2.36540e-03, 2.48036e-03, 2.60090e-03, 2.60090e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 9.56070e-03, 9.56070e-03, 1.00000e-02, 1.07394e-02, 1.07394e-02, 1.10018e-02, 1.12707e-02, 1.12707e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 6.53508e-02, 6.53508e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.73510e-03, 1.73510e-03, 1.76391e-03, 1.79320e-03, 1.79320e-03, 2.00000e-03, 2.19400e-03, 2.19400e-03, 2.32730e-03, 2.46870e-03, 2.46870e-03, 2.58558e-03, 2.70800e-03, 2.70800e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 9.88110e-03, 9.88110e-03, 1.00000e-02, 1.11361e-02, 1.11361e-02, 1.14055e-02, 1.16815e-02, 1.16815e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 6.74164e-02, 6.74164e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.80920e-03, 1.80920e-03, 1.84014e-03, 1.87160e-03, 1.87160e-03, 2.00000e-03, 2.28100e-03, 2.28100e-03, 2.42350e-03, 2.57490e-03, 2.57490e-03, 2.69447e-03, 2.81960e-03, 2.81960e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.02068e-02, 1.02068e-02, 1.08548e-02, 1.15440e-02, 1.15440e-02, 1.18186e-02, 1.20998e-02, 1.20998e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 6.95250e-02, 6.95250e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.82240e-03, 1.82240e-03, 1.88459e-03, 1.94890e-03, 1.94890e-03, 2.00000e-03, 2.36730e-03, 2.36730e-03, 2.51955e-03, 2.68160e-03, 2.68160e-03, 2.80386e-03, 2.93170e-03, 2.93170e-03, 3.00000e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.05353e-02, 1.05353e-02, 1.12245e-02, 1.19587e-02, 1.19587e-02, 1.22394e-02, 1.25267e-02, 1.25267e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 7.16764e-02, 7.16764e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 1.96010e-03, 1.96010e-03, 2.00000e-03, 2.03080e-03, 2.03080e-03, 2.23385e-03, 2.45720e-03, 2.45720e-03, 2.61935e-03, 2.79220e-03, 2.79220e-03, 3.00000e-03, 3.04850e-03, 3.04850e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.08709e-02, 1.08709e-02, 1.16033e-02, 1.23850e-02, 1.23850e-02, 1.26731e-02, 1.29680e-02, 1.29680e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 7.38708e-02, 7.38708e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.04040e-03, 2.04040e-03, 2.07790e-03, 2.11610e-03, 2.11610e-03, 2.32326e-03, 2.55070e-03, 2.55070e-03, 2.72382e-03, 2.90870e-03, 2.90870e-03, 3.00000e-03, 3.17370e-03, 3.17370e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.12154e-02, 1.12154e-02, 1.19928e-02, 1.28241e-02, 1.28241e-02, 1.31179e-02, 1.34185e-02, 1.34185e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 7.61110e-02, 7.61110e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.12160e-03, 2.12160e-03, 2.16138e-03, 2.20190e-03, 2.20190e-03, 2.41348e-03, 2.64540e-03, 2.64540e-03, 3.00000e-03, 3.02650e-03, 3.02650e-03, 3.15838e-03, 3.29600e-03, 3.29600e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.15637e-02, 1.15637e-02, 1.23887e-02, 1.32726e-02, 1.32726e-02, 1.35729e-02, 1.38799e-02, 1.38799e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 7.83948e-02, 7.83948e-02, 8.00000e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.20570e-03, 2.20570e-03, 2.24799e-03, 2.29110e-03, 2.29110e-03, 2.50689e-03, 2.74300e-03, 2.74300e-03, 3.00000e-03, 3.14780e-03, 3.14780e-03, 3.28343e-03, 3.42490e-03, 3.42490e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.19187e-02, 1.19187e-02, 1.27940e-02, 1.37336e-02, 1.37336e-02, 1.40398e-02, 1.43528e-02, 1.43528e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 8.07249e-02, 8.07249e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.29490e-03, 2.29490e-03, 2.33947e-03, 2.38490e-03, 2.38490e-03, 2.60577e-03, 2.84710e-03, 2.84710e-03, 3.00000e-03, 3.27850e-03, 3.27850e-03, 3.41712e-03, 3.56160e-03, 3.56160e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.22839e-02, 1.22839e-02, 1.32113e-02, 1.42087e-02, 1.42087e-02, 1.45206e-02, 1.48393e-02, 1.48393e-02, 1.50000e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 8.31023e-02, 8.31023e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.38930e-03, 2.38930e-03, 2.43673e-03, 2.48510e-03, 2.48510e-03, 2.71062e-03, 2.95660e-03, 2.95660e-03, 3.00000e-03, 3.41570e-03, 3.41570e-03, 3.55698e-03, 3.70410e-03, 3.70410e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.26575e-02, 1.26575e-02, 1.36396e-02, 1.46979e-02, 1.46979e-02, 1.50000e-02, 1.53467e-02, 1.53467e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 8.55304e-02, 8.55304e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.48400e-03, 2.48400e-03, 2.53429e-03, 2.58560e-03, 2.58560e-03, 3.00000e-03, 3.06640e-03, 3.06640e-03, 3.30130e-03, 3.55420e-03, 3.55420e-03, 3.69948e-03, 3.85070e-03, 3.85070e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.30352e-02, 1.30352e-02, 1.50000e-02, 1.52000e-02, 1.52000e-02, 1.55269e-02, 1.58608e-02, 1.58608e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 8.80045e-02, 8.80045e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.57960e-03, 2.57960e-03, 2.63305e-03, 2.68760e-03, 2.68760e-03, 3.00000e-03, 3.17690e-03, 3.17690e-03, 3.42677e-03, 3.69630e-03, 3.69630e-03, 3.84472e-03, 3.99910e-03, 3.99910e-03, 4.00000e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.34186e-02, 1.34186e-02, 1.50000e-02, 1.57111e-02, 1.57111e-02, 1.60457e-02, 1.63875e-02, 1.63875e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 9.05259e-02, 9.05259e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.50000e-03, 2.00000e-03, 2.68300e-03, 2.68300e-03, 2.73990e-03, 2.79800e-03, 2.79800e-03, 3.00000e-03, 3.30190e-03, 3.30190e-03, 3.56733e-03, 3.85410e-03, 3.85410e-03, 4.00000e-03, 4.14940e-03, 4.14940e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.38138e-02, 1.38138e-02, 1.50000e-02, 1.62443e-02, 1.62443e-02, 1.65882e-02, 1.69393e-02, 1.69393e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 9.31050e-02, 9.31050e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.02078e-03, 1.04200e-03, 1.04200e-03, 1.50000e-03, 2.00000e-03, 2.78670e-03, 2.78670e-03, 2.84705e-03, 2.90870e-03, 2.90870e-03, 3.00000e-03, 3.42600e-03, 3.42600e-03, 4.00000e-03, 4.00800e-03, 4.00800e-03, 4.15963e-03, 4.31700e-03, 4.31700e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.42135e-02, 1.42135e-02, 1.50000e-02, 1.67847e-02, 1.67847e-02, 1.71352e-02, 1.74930e-02, 1.74930e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 9.57299e-02, 9.57299e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.04738e-03, 1.09700e-03, 1.09700e-03, 1.50000e-03, 2.00000e-03, 2.89240e-03, 2.89240e-03, 3.00000e-03, 3.02150e-03, 3.02150e-03, 3.26957e-03, 3.53800e-03, 3.53800e-03, 4.00000e-03, 4.15900e-03, 4.15900e-03, 4.31748e-03, 4.48200e-03, 4.48200e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.46194e-02, 1.46194e-02, 1.50000e-02, 1.73371e-02, 1.73371e-02, 1.76895e-02, 1.80490e-02, 1.80490e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 9.84040e-02, 9.84040e-02, 1.00000e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.07378e-03, 1.15300e-03, 1.15300e-03, 1.50000e-03, 2.00000e-03, 2.99990e-03, 2.99990e-03, 3.00000e-03, 3.13620e-03, 3.13620e-03, 3.38938e-03, 3.66300e-03, 3.66300e-03, 4.00000e-03, 4.32700e-03, 4.32700e-03, 4.48656e-03, 4.65200e-03, 4.65200e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.50312e-02, 1.50312e-02, 1.64060e-02, 1.79065e-02, 1.79065e-02, 1.82691e-02, 1.86390e-02, 1.86390e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.01137e-01, 1.01137e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.02840e-03, 1.05760e-03, 1.05760e-03, 1.13049e-03, 1.20840e-03, 1.20840e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.10490e-03, 3.10490e-03, 3.17584e-03, 3.24840e-03, 3.24840e-03, 3.50960e-03, 3.79180e-03, 3.79180e-03, 4.00000e-03, 4.48950e-03, 4.48950e-03, 4.65278e-03, 4.82200e-03, 4.82200e-03, 5.00000e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.54444e-02, 1.54444e-02, 1.68961e-02, 1.84843e-02, 1.84843e-02, 1.88568e-02, 1.92367e-02, 1.92367e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.03922e-01, 1.03922e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.03923e-03, 1.08000e-03, 1.08000e-03, 1.17069e-03, 1.26900e-03, 1.26900e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.21900e-03, 3.21900e-03, 3.29373e-03, 3.37020e-03, 3.37020e-03, 3.62962e-03, 3.90900e-03, 3.90900e-03, 4.00000e-03, 4.65600e-03, 4.65600e-03, 5.00000e-03, 5.00200e-03, 5.00200e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.58710e-02, 1.58710e-02, 1.74031e-02, 1.90832e-02, 1.90832e-02, 1.94579e-02, 1.98400e-02, 1.98400e-02, 2.00000e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.06756e-01, 1.06756e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.08088e-03, 1.16830e-03, 1.16830e-03, 1.24630e-03, 1.32950e-03, 1.32950e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.33200e-03, 3.33200e-03, 3.41048e-03, 3.49080e-03, 3.49080e-03, 4.00000e-03, 4.04610e-03, 4.04610e-03, 4.42089e-03, 4.83040e-03, 4.83040e-03, 5.00000e-03, 5.18230e-03, 5.18230e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.63003e-02, 1.63003e-02, 1.79166e-02, 1.96932e-02, 1.96932e-02, 2.00000e-02, 2.04721e-02, 2.04721e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.09651e-01, 1.09651e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.00334e-03, 1.00670e-03, 1.00670e-03, 1.11018e-03, 1.22430e-03, 1.22430e-03, 1.30316e-03, 1.38710e-03, 1.38710e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.44180e-03, 3.44180e-03, 3.52548e-03, 3.61120e-03, 3.61120e-03, 4.00000e-03, 4.17380e-03, 4.17380e-03, 5.00000e-03, 5.00090e-03, 5.00090e-03, 5.18067e-03, 5.36690e-03, 5.36690e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.67331e-02, 1.67331e-02, 2.00000e-02, 2.03137e-02, 2.03137e-02, 2.07054e-02, 2.11046e-02, 2.11046e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.12601e-01, 1.12601e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    [1.00000e-03, 1.02220e-03, 1.04490e-03, 1.04490e-03, 1.15314e-03, 1.27260e-03, 1.27260e-03, 1.35409e-03, 1.44080e-03, 1.44080e-03, 1.50000e-03, 2.00000e-03, 3.00000e-03, 3.55170e-03, 3.55170e-03, 3.63859e-03, 3.72760e-03, 3.72760e-03, 4.00000e-03, 4.30340e-03, 4.30340e-03, 5.00000e-03, 5.18220e-03, 5.18220e-03, 5.36198e-03, 5.54800e-03, 5.54800e-03, 6.00000e-03, 8.00000e-03, 1.00000e-02, 1.50000e-02, 1.71663e-02, 1.71663e-02, 2.00000e-02, 2.09476e-02, 2.09476e-02, 2.13487e-02, 2.17574e-02, 2.17574e-02, 3.00000e-02, 4.00000e-02, 5.00000e-02, 6.00000e-02, 8.00000e-02, 1.00000e-01, 1.15606e-01, 1.15606e-01, 1.50000e-01, 2.00000e-01, 3.00000e-01, 4.00000e-01, 5.00000e-01, 6.00000e-01, 8.00000e-01, 1.00000e+00, 1.25000e+00, 1.50000e+00, 2.00000e+00, 3.00000e+00, 4.00000e+00, 5.00000e+00, 6.00000e+00, 8.00000e+00, 1.00000e+01, 1.50000e+01, 2.00000e+01]
    };

    %load E,mu
    E = E_cell{i}';
    mu = mu_cell{i}';

    %remove discontinuity
    [~,i] = unique(E);
    j = setdiff( 1:numel(E), i );
    E(j) = E(j) + 1e-12;

    %NIST X-ray beam energy levels [MeV]
    E1 = linspace(-3,log10(8),1000)'; %in log10 space

    %interpolate
    mu1 = interp1(log10(E),log10(mu),E1);
    mu1 = 10.^mu1;
end